Дипломная работа: Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

Тогда

т.е. (ABCD) = (A'B'C'D').

Замечание.

Пусть A'= (A). Имеем

Откуда, перемножив, получаем

и .

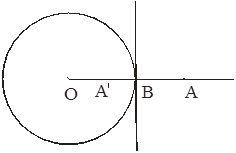
Зафиксируем точку В, а r пусть неограниченно возрастает, тогда |AB|=|A'B|, т.е. инверсия относительно „окружности бесконечно большого радиуса" есть симметрия относительно прямой.

2. Аналитическое задание инверсии

Пусть A'= (A), где АO, А. Введём на плоскости декартову прямоугольную систему координат так, чтобы её начало совпало с точкой О.

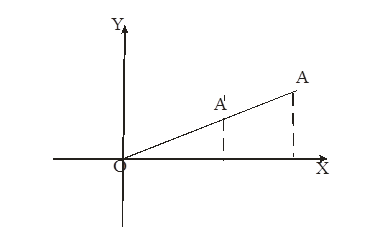
Пусть x, y - координаты точки А, x', y'-координаты точки А'. Выразим х и у через х' и у'. Имеем А' [OA) и

,

.

Очевидным образом получаем

,

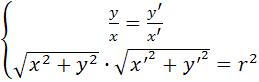откуда находим

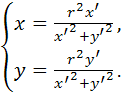(1)

3. Преобразование окружности и прямой при инверсии

Пусть (O, r) П. Рассмотрим окружность SП. Найдём (S).

Введём на плоскости систему координат хОу. Пусть в этой системе координат окружность S имеет уравнение

A () +Bx+Cy+D=0 (2)

Подвергнем S инверсии . Подставляя в (2) вместо х и у их выражения из (1), получим

A+Bx'+Cy'+D () =0 (3)

Если D=0, т.е. если OS, то (S) - прямая, не проходящая через О.

Если D0, т.е. если OS, то (S) - окружность, не проходящая через точку О.

Итак, доказана.