Дипломная работа: Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

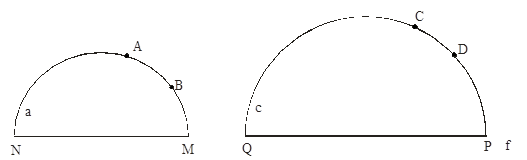
Рассмотрим упорядоченные четвёрки точек A, B, M, N и C, D, P, Q.

Доказательство.1 ) Пусть . Докажем, что (ABMN ) = (CDPQ ).

Т.к. , то существует неевклидово движение , такое, что . Остаётся показать, что . Учитывая, что - конечная цепочка инверсий с центрами на f, и каждая инверсия сохраняет величину угла, имеем .

Т. к.

, то ,.

Итак, (ABMN) = ( CDPQ).

Пусть (ABMN) = ( CDPQ ). Докажем, что .

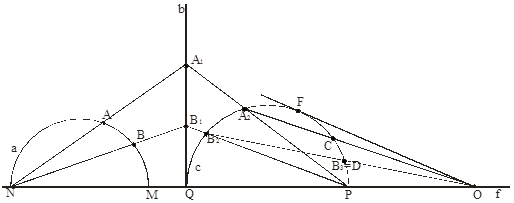
Рассмотрим

;

тогда

,

Рассмотрим

;

тогда

, .

Рассмотрим , где , (OF) - касательная из точки О к с . Тогда , , .

Покажем, что .

Имеем , , тогда (ABMN) = ( C PQ).

Учитывая условие теоремы, получаем (CDPQ ) = (C), откуда , т.е. D и принадлежат окружности Аполлония (), которая пересекает с в единственной точке, поэтому .

Итак, существует неевклидово движение , такое, что т.е. .

Замечание 2. Критерий конгруэнтности углов на модели Пуанкаре.

Пусть - евклидова величина неевклидова угла (а, b ), - евклидова величина неевклидова угла (c, d ).

.

Доказательство.1 ) Пусть , тогда существует неевклидово движение :

Т. к. - это конечная цепочка инверсий, а инверсия сохраняет величину углов, то .