Дипломная работа: Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

1 случай

2 случай

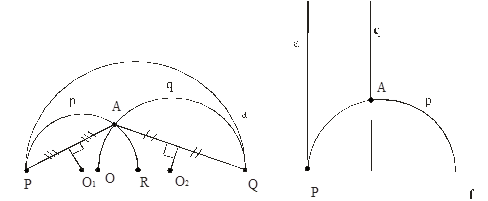
Построим евклидову полуокружность, ортогональную f и проходящую через точки P и A . Л-прямая p проходит через точку А и не пересекает а.

Аналогично строим Л-прямую q , проходящую через точку А и не пересекающую а .

Итак, существуют две Л-прямые p и q , проходящие через Л-точку А и не пересекающие Л-прямую а .

Замечание. Очевидно, что любая евклидова полуокружность, ортогональная f и проходящая через точку А и любую точку евклидова отрезка QR , не пересекает а. Таким образом, существует бесчисленное множество Л-прямых, проходящих через точку А и не пересекающих Л-прямую а.

Итак, доказана непротиворечивость геометрии Лобачевского.

В следующем параграфе покажем осуществление некоторых вопросов геометрии Лобачевского на модели Пуанкаре, где также используется инверсия.