Дипломная работа: Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

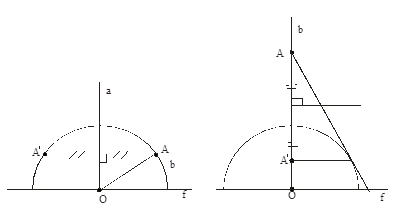
- евклидовы касательные к a и b соответственно в точке А.

- евклидова биссектриса

и .

c= ( O, OA) - неевклидова биссектриса .

Доказательство основано на критерии конгруэнтности углов на модели Пуанкаре.

Задача 3. Дана Л-прямая а в точке А, не лежащая на а . Построить Л-прямую b , ортогональную а, и .

1 случай

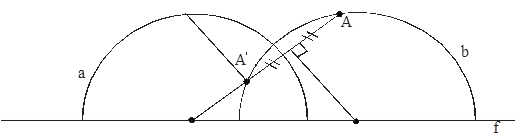
Достаточно построить и тогда b- неевклидова прямая, проходящая через точки А и , т.к окружность, проходящая через пару инверсных точек, ортогональна окружности инверсии.

2 случай

3 случай

( O, OA) = b

Задача 4. Построить высоту, медиану, биссектрису в треугольнике.

Решение основано на задачах 1-3.

Проверим выполнимость аксиомы непрерывности в формулировке Дедекинда.

IV. Пусть все точки прямой разбиты на два класса так, что выполняются условия:

Оба класса не пустые;

Каждая точка прямой отнесена к одному и только одному из классов;

Каждый класс есть выпуклое множество.

Покажем, что в одном из классов существует граничная точка, т.е. такая точка, которая не лежит между двумя точками одного и того же класса.

Пусть все точки Л-прямой а разбиты на два класса и так, что выполнены условия 1-3 аксиомы Дедекинда.

Рассмотрим евклидову прямую , касающуюся Л-прямой a и параллельную f.

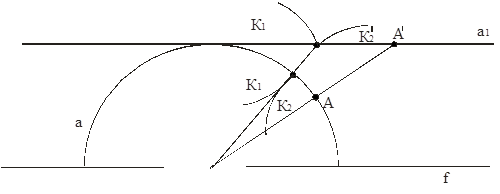
Установим соответствие между точками прямых а и , с помощью радиальных прямых. Очевидно, что это соответствие будет взаимно-однозначным. Поэтому все точки евклидовой прямой разобьются на два класса и так, что будут выполнены условия 1-3 аксиом Дедекинда.

Т.к. для евклидовой прямой аксиома Дедекинда справедлива, то в одном из классов или существует граничная точка .

Тогда соответствующая ей точка будет граничной в разбиении Л-прямой а.

Проверим выполнимость аксиомы Лобачевского на модели Пуанкаре.

V. Пусть дана Л-прямая а и Л-точка А, не принадлежащая а.