Дипломная работа: Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

рис. 1

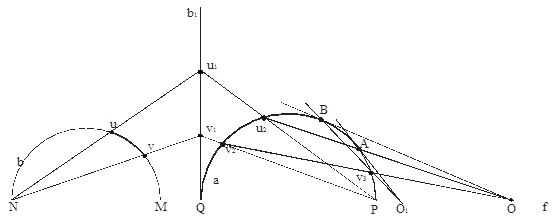
Рис.2

Рассмотрим

;

тогда

Рассмотрим

,

тогда

.

Рассмотрим

где ,

(OF) - касательная из точки О к а , тогда

(),

Из , то цепочку симметрий оборвём и (см. рис.1).

Если , то рассмотрим ещё одну симметрию

-

касательная к а в точке А (см. рис.2).

Итак, имеем неевклидово движение , преобразующее u в А, v в В, т.е.

[AB] [uv ].

Докажем, что [AB] [BA].

Рассмотрим

, где

- касательная из точки к а, тогда а= I ( a), B= I ( A), A= I ( B).

Итак, имеем неевклидово движение , преобразующее

А в В, В в А, т.е. [AB ] [BA ].

Прежде чем продолжить проверку аксиом конгруэнтности, рассмотрим