Дипломная работа: Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

Т.к. , то существует неевклидово движение , преобразующее стороны в стороны .

1) Пусть , .Т. к.

,, то , , т.е. и , , откуда , .

2) Пусть , .

Рассмотрим инверсию относительно биссектрисы . Тогда приходим к ситуации 1).

Замечание. На следующих рисунках изображены конгруэнтные между собой треугольники ABC и .

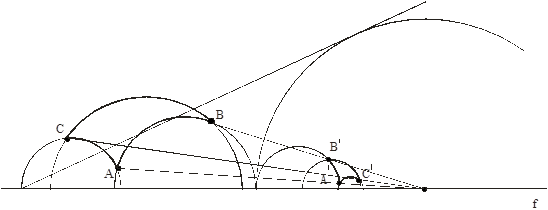
рис. 1

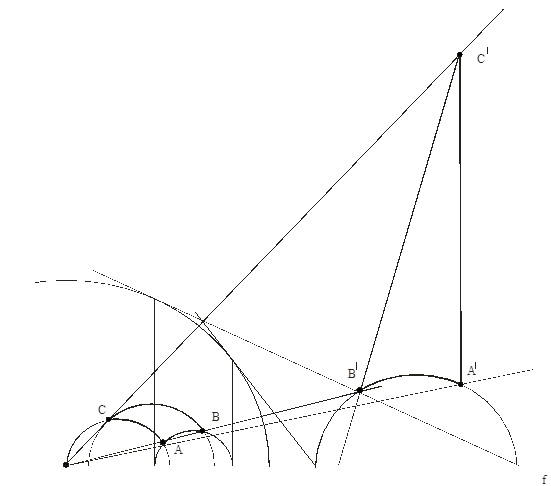
рис. 2

Рассмотрим далее решение некоторых задач на модели.

Задача 1. Построить середину отрезка АВ.

1 случай

- касательная к а из О. Докажем, что . Для этого достаточно рассмотреть

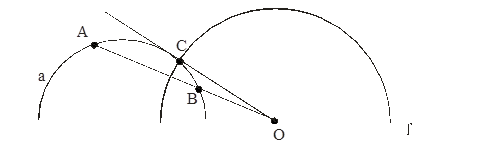
2 случай

Строим евклидову окружность S с диаметром ОВ.

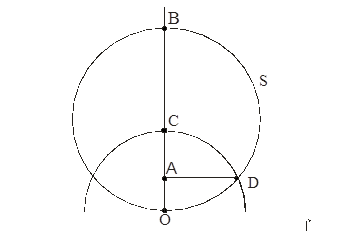
Для доказательства того, что

достаточно рассмотреть

.

Заметим, что т.к.

,

то неевклидова середина отрезка АВ „тяжелее” евклидовой.

Задача 2. Построить биссектрису угла (a, b).