Дипломная работа: Парадокси в математичній статистиці

Часто розглядають не одну оцінку , побудовану за вибіркою , а послідовність оцінок У цій ситуації природно говорити про асимптотичну поведінку послідовності оцінок.

Означення. Послідовність оцінок будемо називати спроможною послідовністю оцінок параметра , якщо для кожного

при , або, що те саме, збігається за ймовірністю до , при .

Означення. Послідовність оцінок називатимемо асимптотично незміщеною послідовністю оцінок параметра , якщо при , або, що те саме, при .

Оцінки мінімальної дисперсії.

Основне питання задачі оцінювання параметрів розподілів - наскільки великою є похибка при заміні параметра оцінкою .

Оцінки , що пропонуються для оцінювання параметра , повинні бути незміщеними, тобто .

Такі оцінки мають меншу міру розсіювання відносно порівняно з оцінками, для яких .

Для оцінювання параметра можна запропонувати багато незміщених оцінок. Із сукупності таких оцінок природно вибрати ті, що мають мінімально можливу міру розсіювання (дисперсію).

Означення. Незміщену оцінку параметра будемо називати його найкращою оцінкою, оцінкою мінімальної дисперсії або ефективною оцінкою , якщо .

У зв’язку з цим означенням природно виникає питання: наскільки малою може бути мінімально можлива дисперсія оцінки (наскільки малими можуть бути відхилення від )? Виявляється, що коли сукупність розподілів , вибірки досить регулярно залежить від оцінюваного параметра , то можна вказати нижню межу дисперсії всіх незміщених оцінок параметра (нерівність Крамера - Рао). У деяких випадках існують оцінки параметра, на яких нижня межа досягається. Ці оцінки є ефективними. Порівнюючи дисперсію даної оцінки з нижньою межею дисперсій незміщених оцінок, можна з’ясувати, наскільки оцінка близька до найкращої можливої. Докладніше.

Нехай вибірка фіксованого обсягу має щільність розподілу .

Параметр будемо вважати одновимірним, а щодо множини його можливих значень припустимо, що вона є скінченим інтервалом числової прямої.

Лема 1.2.1 Якщо майже для всіх існують похідні

і , ,

мажорові інтегрованими функціями:

і виконуються умови

; , ,

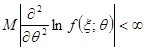то для всіх

Означення. Функцію

(коли вона визначена) називають інформацією за Фішером .

У лемі 1.2.1 наведено достатні умови, за яких інформація існує. Зазначимо, що

Теорема 1.2.1 (нерівність Крамера - Рао). Нехай задовольняються умови леми 1.2.1 і

незміщена оцінка параметра така, що функція