Дипломная работа: Парадокси в математичній статистиці

,

.

Розділ ІІ. Парадокси в математичній статистиці

2.1 Парадокс оцінок математичного сподівання

2.1.1 Історія парадоксу

Зрівнювання протилежних значень і відхилень в "середньому", тобто підсумовування спостережень до одного значення має давні традиції. Есхіл писав у трагедії "Евменіди": "Богу завжди середина люб'язна, і міру поважає божество", а послідовники китайського філософа Конфуція говорять, що "у нерухомості середнього є найбільша досконалість". Поняття "середнього" можна інтерпретувати в різний спосіб (середнє арифметичне, середнє геометричне, медіана і т. ін). Але у практичних застосуваннях протягом тривалого часу вкрай важливу роль відігравало середнє арифметичне. Вже в перших результатах теорії ймовірностей і математичної статистики вивчалося середнє арифметичне вибірки.

2.1.2 Парадокс

Нехай - реалізація вибірки з розподілу . Розподіл залежить від параметра , що набуває значень з деякої множини можливих значень . Значення параметра в розподілі невідомо, і його необхідно оцінити за реалізацією вибірки .

Якщо за розподіл обрати нормальний розподіл , то оцінка

незміщена, спроможна, ефективна оцінка для параметра . Для розподілу ж , відмінного від нормального, оцінка не є незміщеною оцінкою з найменшою дисперсією.

У цьому і полягає парадокс оцінки математичного сподівання.

2.1.3 Пояснення парадоксу

Нехай - вибірка з нормального розподілу з параметрами . Порахуємо математичне сподівання оцінки :

тому - незміщена оцінка для параметра .

З’ясуємо, чи є спроможною оцінкою параметра , тобто чи збігається за ймовірністю до . Для досить малих маємо:

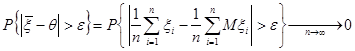
в силу закону великих чисел. Останнє означає, що є спроможною оцінкою параметра .

Покажемо, що незміщена оцінка з найменшою дисперсією:

.

Умова обертання нерівності Крамера - Рао (дивитися підрозділ 1.2) в рівність говорить, що якщо статистика , така, що

де - щільність розподілу вибірки , то - незміщена й ефективна оцінка параметра .

Обчислимо :

== ==

== ==

=== =

= = ,

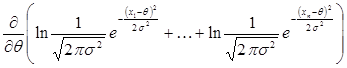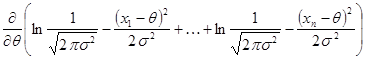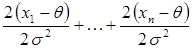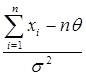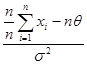тому - ефективна оцінка для параметра .

Розглянемо сім’ю розподілів на , які залежать від параметра і задаються щільністю , .

Кількість інформації за Фішером визначимо

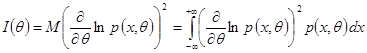. (2.1.3.1)

За умов, що ми вважаємо, що підінтегральний вираз дорівнює нулеві. Отже,