Дипломная работа: Парадокси в математичній статистиці

Наслідок 1. Якщо оцінка задовольняє умови теореми і для неї нерівність Крамера – Рао

перетворюється на рівність, то є ефективною оцінкою параметра .

Наслідок 2. Якщо оцінка задовольняє умови теорем, а статистика - умову

де - розподіл вибірки , то - незміщена й ефективна оцінка параметра .

Наслідок 3. Нехай - вибірка з дискретного розподілу і для сумісного розподілу

випадкових величини виконані умови теореми, тоді нерівність Крамера - Рао можна записати у вигляді

.

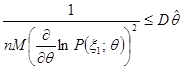1.3 Метод максимальної правдоподібності

Нехай - вибірка із розподілом , що залежить від параметра Параметр невідомий і його необхідно оцінити за вибіркою .

Означення. Функцією максимальної правдоподібності вибірки будемо називати функцію параметра , що визначається рівністю , , якщо вибірковий вектор абсолютно неперервний зі щільністю і рівністю , , якщо вибірковий вектор дискретний з розподілом .

Метод максимальної правдоподібності побудови оцінок полягає в тому, що за оцінку параметра вибирається точка , в якій функція максимальної правдоподібності досягає найбільшого значення.

Означення. Оцінкою максимальної правдоподібності будемо називати точку , в якій функція максимальної правдоподібності досягає найбільшого значення.

Іншими словами, оцінкою максимальної правдоподібності параметра будемо називати відмінні від константи розв’язки рівняння

,

якщо такі розв’язки існують. Корені, які не залежать від вибірки , тобто мають вигляд , де - константа, слід відкинути (оцінка - це функція вибірки).

Логарифм від функції максимальної правдоподібності називають логарифмічною функцією максимальної правдоподібності.

Зазначимо, що функції та досягають найбільшого значення в одній і тій самій точці. А відшукати точку, в якій функція досягає найбільшого значення, часто зручніше.

Якщо функція диференційована по , то для того щоб розв’язати рівняння

(1.3.1)

достатньо знайти стаціонарні точки функції

,

розв’язуючи рівняння

і, порівнюючи значення функції у стаціонарних точках і на межі множини , вибрати точку , в якій функція , досягає найбільшого значення. Ця точка і буде розв’язком рівняння (1.3.1).

Рівняння

називають рівняннями максимальної правдоподібності.