Дипломная работа: Парадокси в математичній статистиці

мажоровна інтегрованою функцією:

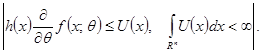Тоді (1.2.1)

причому рівність в (1.2.1) досягається тоді і тільки тоді, коли можна подати у вигляді

Наслідок 1. Якщо оцінка задовольняє умови теореми і для неї нерівність Крамера – Рао перетворюється на рівність, то є ефективною оцінкою параметра .

Наслідок 2. Якщо оцінка задовольняє умови теореми, а статистика - умову

де - щільність розподілу вибірки , то - незміщена й ефективна оцінка параметра .

Наслідок 3. Нехай вибірка з розподілу з щільністю , причому для сумісної щільності

випадкові величини виконані умови теореми. Тоді нерівність Крамера - Рао можна переписати у вигляді

.

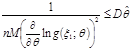1.1 Нерівність Крамера - Рао (розподіл дискретний)

Нерівність Крамера - Рао і твердження, аналогічні наведеним вище, мають місце також тоді, коли розподіл вибірки дискретний, тобто існує не більше ніж злічена множина точок , для яких

Лема 1.2.2 (розподіл дискретний).

Якщо для всіх можливих значень вибірки існують похідні

і , ,

Ряди

і

збігаються абсолютно й рівномірно відносно і виконуються умови

,

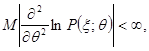
то для всіх

1.2 Теорема 1.2.2 (нерівність Крамера - Рао, розподіл дискретний)

Нехай задовольняються умови леми 1.2.2 і - незміщена оцінка параметра така, що для всіх можливих значень вибірки ряд

збігається абсолютно й рівномірно відносно . Тоді

причому рівність справджується тоді, коли можна подати у вигляді