Дипломная работа: Разработка системы управления многосвязных систем автоматического регулирования исполнительного уровня

,

,

,

Не все корни характеристического уравнения замкнутой системы левые, следовательно, система неустойчива.

Колебательная граница устойчивости

С помощью обобщенного годографа Найквиста подберем такую пару значений параметров К₁ и К₂ , при которых МСАР находится на колебательной границе устойчивости.

Значения параметров и , при которых МСАР находится на колебательной границе устойчивости, следующие:

,

.

Изобразим годограф Найквиста системы с найденными коэффициентами в области высоких частот (Рисунок 1.15).

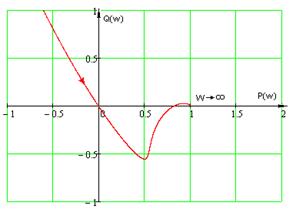
Рисунок 1.15 – Обобщенный годограф Найквиста при ,

Проверим правильность найденных значений моделированием МСАР (Приложение 5). Графики переходных процессов, полученные в результате моделирования, представим на рисунке 1.16.

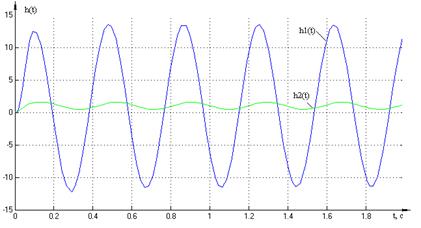
Рисунок 1.16 – Переходные характеристики

Графики переходных характеристик представляют собой незатухающие колебания, следовательно, при заданных параметрах система находится на границе устойчивости.

Влияние перекрестных связей на точность МСАР в установившемся режиме

Запишем передаточную матрицу замкнутой системы, изображенной на рисунке 1.10.

,

где W( p) – передаточная матрица разомкнутой системы (1.15), определенная в пункте 1.3.1.

Рассматриваемая система имеет два входа и два выхода, следовательно, передаточная матрица замкнутой системы имеет вид:

. (1.20)

Передаточная матрица замкнутой системы, соответствующая паре «вх .1 – вых .1», – , паре «вх .1 – вых .2», – .

Построим АЧХ замкнутой МСАР относительно пар «вх .1 – вых .1» и «вх .1 – вых .2» с помощью программного пакета MathCAD (Приложение 6а).

,

.

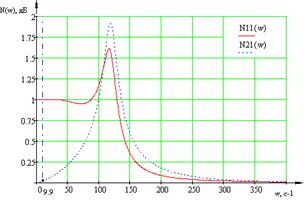
Рисунок 1.17 – АЧХ замкнутой МСАР относительно пар «вх .1 – вых .1» и «вх .1 – вых .2»

Определим ординаты построенных характеристик на частоте :

,

.