Дипломная работа: Регресійний аналіз інтервальних даних
![]()
Припустимо, що n досить велике і можна вважати, що власні числа матриці о(1/n) менше одиниці по модулю, тоді
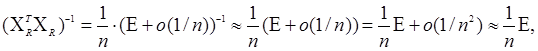
що і було потрібно довести.
Підставимо доведене асимптотичне співвідношення у формулу для приросту![]() *,одержимо
*,одержимо
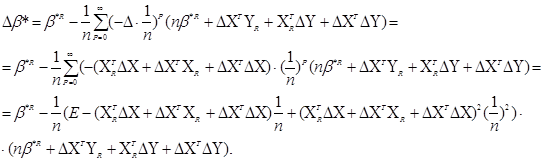
Виразимо Δ![]() * відносно приросту ΔХ, ΔY до 2-гo порядку
* відносно приросту ΔХ, ΔY до 2-гo порядку
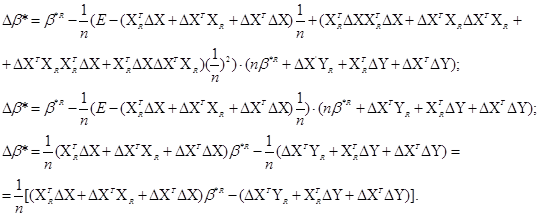
Перейдемо від матричної до скалярної форми, опускаючи індекс (R):
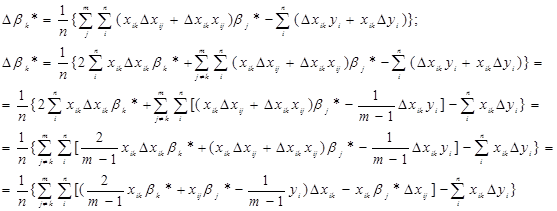
Будемо шукати max(|Δ ![]() k * |) по Δxij і Δyi (i=1,…, п;j=1,…, m). Для цього розглянемо всі три раніше введених типи обмежень на похибки виміру.
k * |) по Δxij і Δyi (i=1,…, п;j=1,…, m). Для цього розглянемо всі три раніше введених типи обмежень на похибки виміру.
Тип 1 (абсолютні похибки виміру обмежені). Тоді:
![]()
Тип 2 (відносні похибки виміру обмежені). Аналогічно одержимо:
![]()
Тип З (обмеження накладені на суму похибок). Припустимо, що |Δ ![]() k * | досягає максимального значення при таких значеннях погрішностей Δxij і Δyi ,
k * | досягає максимального значення при таких значеннях погрішностей Δxij і Δyi ,
які ми позначимо як:
![]()
тоді:
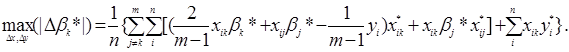
Через лінійність останнього вираження і виконання обмеження типу 3:

Для спрощення запису зробимо наступні заміни:

Тепер для досягнення поставленої мети можна сформулювати наступне завдання, що розділяється на m типових завдань оптимізації:

при обмеженнях

Перепишемо функції, що мінімізуємо, в наступному вигляді: