Дипломная работа: Регресійний аналіз інтервальних даних

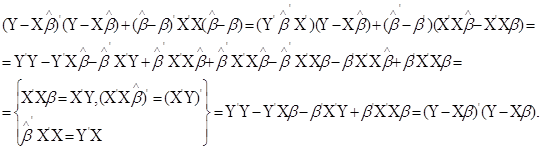
Ліва частина тотожності мінімальна якщо .

Регресію будемо позначати .

Залишок

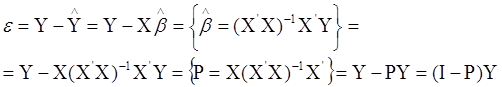
Мінімальне значення суми квадратів залишків називають залишковою сумою квадратів (RSS).

Застосуємо формулу (2.1), RSS перепишеться:

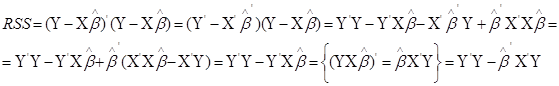
Якщо застосувати формулу (2.2), отримаємо:

.

Оцінки та єдині.

Розділ ІІ. Довірчі інтервали регресії. Похибка прогнозу

Нехай прогнозоване значення визначається по рівнянню регресії з оціненими параметрами

(2.1)

В силу того, що - незміщені оцінки деяких невідомих параметрів відповідного взаємозв'язку, - одне з можливих значень прогнозованої величини при заданих значеннях , точніше - це оцінка середнього значення . Оскільки випадкова величина, то і оцінка також випадкова і має дисперсію. Визначимо її значення.

Використавши теорему про дисперсії суми залежних величин, одержимо:

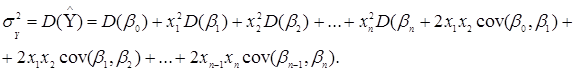
Перепишемо у вигляді:

де - вектор заданих значень незалежних змінних. Звідки одержимо:

Оскільки значення нам відомо, то введемо в останню формулу її оцінку , звідки дисперсія буде:

(2.2)

Таким чином, середнє значення лежить у межах:

(2.3)

Розділ ІІІ. Лінійний регресійний аналіз інтервальних даних

Перейдемо до багатомірного статистичного аналізу. Спочатку з позиції асимптотичної математичної статистики інтервальних даних розглянемо оцінки методу найменших квадратів (МНК).