Дипломная работа: Регресійний аналіз інтервальних даних

Розділ І. Лінійна багатовимірна регресія

Нехай- деяка випадкова величина, флуктує навколо деякого невідомого значення параметра , тобто , де- флуктуація або похибка. Наприклад, похибка може бути властива самому експерименту, або похибка може виникати при вимірювані невідомого параметра .

Припустимо тепер, що можна представити у вигляді

де - відомі постійні величини, а – невідомі параметри, які потрібно оцінити.

Якщо величина змінюється і при цьому змінна набуває значень , тобто можна записати

(1.1)

У матричному вигляді, отримаємо:

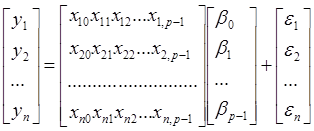
Або

(1.2)

де .

Означення : Матриця розміру називається регресійною матрицею . При цьому її елементи обираються таким чином, щоб , тобто число лінійних незалежних стовпців дорівнювало , також матрицю називають матрицею повного рангу.

Але в деяких випадках приймає лише два значення 0, 1, тоді можливі випадки коли в матриці деякі рядки або стовпці збігаються, тобто є лінійно – залежними. В цьому випадку називають матрицею плану . Змінні називають регресорами (j=1,…,p-1), або предикторними змінними , а - називають відкликом.

Модель (1) або (2) лінійна відносно невідомих параметрів. Тому її називають лінійною моделлю .

Перед тим як оцінювати вектор , замітимо, що вся теорія будується для моделі (2).

Для оцінки невідомих параметрів використовують метод найменших квадратів (МНК), який полягає в мінімізації суми квадратів залишків. Необхідно мінімізувати величину:

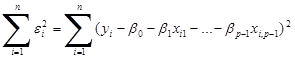(1.3)

за параметрами . Вираз (1.3) запишеться так:

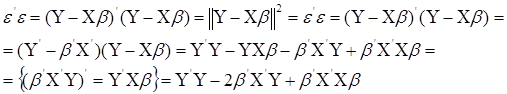(1.4)

Шукаємо градієнт :

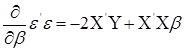
Розв’язуємо рівняння:

Таким чином

(1.5)

Необхідно перевірити, що знайдена стаціонарна точка є точкою мінімуму функції . Справедлива така тотожність