Дипломная работа: Регресійний аналіз інтервальних даних
Тип 2. Відносні погрішності виміру обмежені:
Тип 3. Обмеження накладені на суму погрішностей:
Перейдемо до обчислення нотни оцінки МНК. Справедлива рівність:
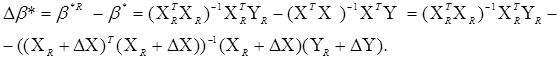
Скористаємося наступною теоремою з теорії матриць.
Теорема . Якщо функція f(λ) розкладається в степеневий ряд у колі збіжності |λ – λ0 | < r, тобто
то це розкладання зберігає силу, якщо скалярний аргумент замінити будь-якою матрицею А, характеристичні числа якої λk , k = 1,…,n , лежать всередині кола збіжності.
Легко переконатися, що:
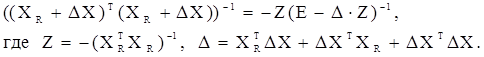
Це випливає з послідовності рівностей:
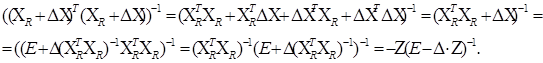
Застосуємо наведену вище теорему з теорії матриць, припускаючи
А = Δ Z і приймаючи, що власні числа цієї матриці задовольняють нерівності |λk |< 1. Тоді одержимо:
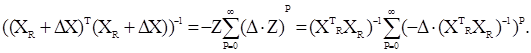
Підставивши останнє співвідношення на закінчення згаданої теореми, одержимо:
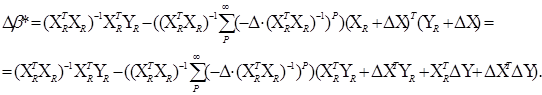
Для подальшого аналізу знадобиться допоміжне твердження. Виходячи із припущень 1-3, доведемо, що:
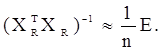
Доведення. Справедлива рівність
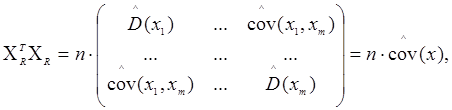
де 
- спроможні і незміщені оцінки дисперсій і коефіцієнтів коваріації, тобто
тоді
де 