Дипломная работа: Регресійний аналіз інтервальних даних

- помилки спостережень некорельовані, тобто .

Тоді, як відомо, оцінки МНК є найкращими лінійними оцінками, тобто спроможними і незміщеними оцінками, які являють собою лінійні функції результатів спостережень і мають мінімальні дисперсії серед безлічі всіх лінійних незміщених оцінок. Далі саме цей найбільше практично важливий окремий випадок розглянемо більш докладно.

Запишемо істині дані в наступній формі:

де R - індекс, що вказує на те, що значення істинне. Істині і обмірювані дані пов’язані таким чином:

де

Припустимо, що похибки виміру відповідають граничним умовам

(3.1.3)

Нехай безліч W можливих значень входить в Z - область визначення функції f (X,Y). Розглянемо - оцінку МНК, розраховану за істинним значенням факторів і відгуку, і - оцінку МНК, знайдену за відхиленими похибкам даних.

Тоді

Введемо поняття нотни.

Означення : Величину максимально можливого (по абсолютній величині) відхилення, викликаного похибками спостережень , відомого статистику значення f(y) від істинного значення f(x), тобто

Nf(x) = sup | f(y) - f(x) | ,

де супремум береться по безлічі можливих значень вектора похибки , будемо називатинотною .

Якщо функція f має частинні похідні другого порядку, а обмеження на похибку мають вигляд

(3.1.4)

причому мало, то збільшення функції f з точністю до нескінченно малих більш високого порядку описується головним лінійним членом, тобто

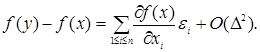
Щоб одержати асимптотичний (при ) вираз для нотни, досить знайти максимум і мінімум лінійної функції (головного лінійного члена) на кубі, заданому нерівностями (4.1.4). Легко бачити, що максимум досягається, якщо покласти

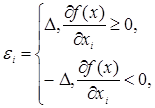
а мінімум, що відрізняється від максимуму тільки знаком, досягається при . Отже, нотна з точністю до нескінченно малих більше високого

порядку має вигляд

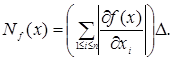(3.1.5)

Цей вираз назвемо асимптотичною нотною .

Покладемо:

Будемо називати n(1) нижньою нотною , а n(2) верхньою нотною .