Дипломная работа: Теореми Чеви і Менелая та їх застосування
Запишемо теорему Менелая для трикутника 
і прямої 
:
 |
.
, 
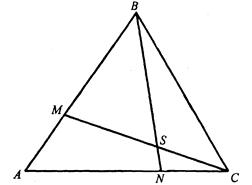Запишемо теорему Менелая для трикутника 
і прямої 
:
,
, 
Відповідь: , .
Задача 1.8 Ортоцентр 
трикутника 
(ортоцентр – точка перетину висот) ділить висоту навпіл. Довести , що 
, де 
– кути трикутника.
Доведення.
 |
?????
- ????? ?????????, - ???? ?????????, 
.
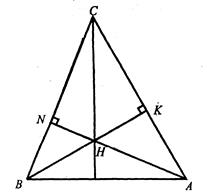Запишемо теорему Менелая для трикутника 
і прямої 
:
Виходячи з умови 
.
З 
.
З 
.
З 
.
Підставимо знайдені залежності в теорему Менелая:
,
,
,
що і треба було довести.
Задача 1.9 З вершини 
прямого кута трикутника 
проведено висоту 
, а в трикутнику
