Дипломная работа: Теореми Чеви і Менелая та їх застосування

З теореми Менелая для трикутника та прямої (точка лежить на , – на , – на ) випливає, що

Аналогічно, з трикутників та , які перетинаються прямими та відповідно, маємо

,

Перемножуючи виписані рівності, після скорочення одержуємо

Але точки лежать на сторонах або продовженнях сторін трикутника і згідно з теоремою Менелая лежать на одній прямій.

Теорема доведена.

Наступна теорема була доведена в другій половині ІІІ століття древнегрецьким математиком Паппом Александрійським.

Теорема Паппа. На одній з прямих, що перетинаються взяті точки , на іншій – точки (див. рис. 8а). Прямі , , перетинаються в точках відповідно. Тоді точки лежать на одній прямій.

Доведення.

Розглянемо трикутник , де – точка перетину прямих , – точка перетину прямих , – точка перетину прямих (див. рис. 8б). Точки лежать на прямих відповідно.

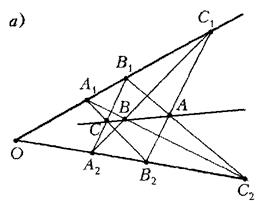
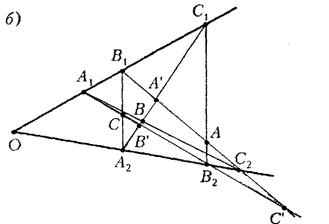
Рис. 1.8

Запишемо теорему Менелая для трикутника та п’яти прямих , які перетинають сторони (або їх продовження) цього трикутника. Маємо

та пряма: ,

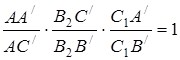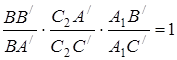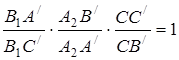та пряма: ,

та пряма: ,

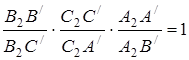та пряма: ,

та пряма: .

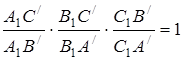Перемножуючи одержані рівності, знаходимо

,

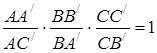отже, точки лежать на одній прямій. Теорема доведена.

Теорема Паскаля. Нехай шестикутник вписано в коло. Тоді точки перетину його протилежних сторін лежать на одній прямій.

Доведення.

Нехай – точки перетину прямих і , і , і відповідно, а – точки перетину прямих і , і , і відповідно (див. рис. 1.9). Необхідно довести, що лежать на одній прямій.

Застосуємо теорему Менелая до трикутника та прямої :

.