Дипломная работа: Теореми Чеви і Менелая та їх застосування

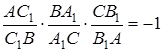
Тут всі відношення, що перемножуються – це відношення орієнтованих відрізків .

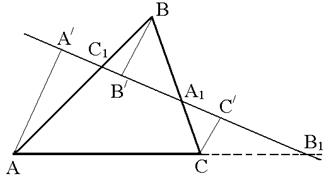
Рис. 1.5

Доведення.

Необхідність. Нехай пряма перетинає прямі та в точках і відповідно (див. рис. 1.5) і – перпендикуляри, які опущено з точок на пряму . Як було доведено раніше,

.

Перемножаючи записані відношення, маємо

.

Достатність. Проведемо пряму . Ми повинні довести, що ця пряма перетинає в точці . Насамперед доведемо, що дійсно перетинає . Припустимо, що паралельна (див. рис. 1.6). Але тоді

Звідси та з рівності (1.1) випливає , що неможливо.

Нехай – точка перетину прямих та . По вже доведеному

Рис. 1.6

Порівнюючи з умовою, одержуємо, що

.

Оскільки мова йде про відношення орієнтованих відрізків, то , що потрібно було довести довести. Отже, теорема Менелая повністю доведена.

Зауваження 1. При розв’язанні конкретних обчислювальних задач, якщо відомо, що точки і лежать на одній прямій, можна не турбуватися про запис відношень орієнтованих відрізків в формулі (1.1), а обмежитися відношеннями їх довжин.

Зауваження 2. Якщо замінити в (1.1) орієнтовані відношення відношеннями довжин, обернена теорема перестає бути вірною, тобто точки і , для яких виконується (1.1), не повинні лежати на одній прямій.

Наприклад, нехай точки взяті на сторонах трикутника так, що , і – середина сторони , тоді

,

але точки не лежать на одній прямій.

1.3 Теореми Дезарга, Паппа, Паскаля, Гаусса

Нетривіальними прикладами використання теореми Менелая є доведення наступних теорем Дезарга, Паппа, Паскаля.

Теорема Дезарга є однією з перших та важливіших теорем проективної геометрії. Вона була доведена в першій половині XVIIстоліття французським математиком та інженером Жераром Дезаргом (1591-1661).

Теорема Дезарга. Трикутники та розташовані на площині так, що прямі мають спільну точку О (див. рис. 1.7). Нехай А – точка перетину пряміх та , В – точка перетину прямих та , С – точка перетинуц прямих та . Тоді точки лежать на одній прямій.

Рис. 1.7