Дипломная работа: Теореми Чеви і Менелая та їх застосування

Запишемо теорему Менелая для трикутника і прямої :

,

,

Звідси см , см.

Запишемо теорему Менелая для трикутника і прямої :

,

Звідси см, (см)

Відповідь: 12 см, 18 см, 30 см.

Задача 1.5 Через середину сторони паралелограма , площа якого дорівнює 1, і вершину проведено пряму, яка перетинає діагональ у точці . Знайти площу чотирикутника .

Розв’язок.

Запишемо теорему Менелая для трикутника і прямої :

,

,

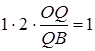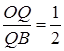
Оскільки площі трикутників з рівними висотами відносяться як основи, то

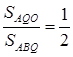
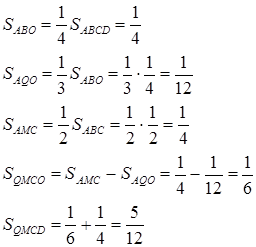
Відповідь:

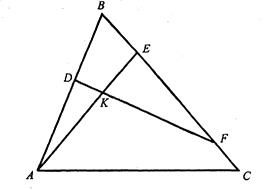
Задача 1.6. У трикутнику на стороні взято точку , а на стороні точки і так , що і . У якому відношенні пряма ділить відрізок .

Розв’язок.

За умовою .

.

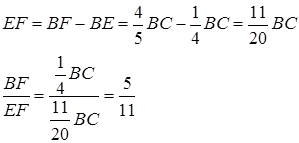
Запишемо теорему Менелая для трикутника і прямої :

,

,

.

Відповідь: 11 : 3.

Задача 1.7 На сторонах і трикутника дано відповідно точки і такі , що .У якому відношенні точка перетину відрізків і ділить кожен з цих відрізків ?