Контрольная работа: Анализ систем автоматического управления
3) Построить графики логарифмических частотных характеристик разомкнутой импульсной системы L * (λ) и φ* (λ) при заданных значениях Т, Т1 , τ1 , γ и выбранном K 0 . По графикам определить запасы устойчивости системы по модулю ∆ L * и фазе ∆φ* .
4) Определить ошибку системы по скорости еск при входном воздействии v ( t )= t (скачок по скорости), а также первые два коэффициента ошибок с0 и с1 .
5) Вычислить переходной процесс в системе при воздействии v ( t )= 1[t] (скачок по положению.
Исходные данные:
Таблица 2. Анализ одноконтурного замкнутого импульса
|
Номер варианта | γ | T | T1 | τ1 |
| 10 | 0.3 | 0.1 | 0.1 | 0,05 |
Анализируется одноконтурная замкнутая импульсная САУ, состоящая из непрерывной части (НЧ) и импульсного элемента (ИЭ), формирующего прямоугольные импульсы длительностью τ=γТ, где Т -период дискретизации, 0≤γ≤1. Исходные данные для расчетов приведены в таблице 2. Передаточная функция непрерывной части имеет вид:
![]()
Импульсный элемент представляется в виде идеального ключа и формирующего устройства с передаточной функцией:
![]()
Структурная схема системы представлена на рис. 2.1. В табл. 2 Т, Т1 , τ -постоянные времени имеют размерность секунды, К0 - коэффициент передачи НЧ имеет размерность сек-1 и выбирается далее.
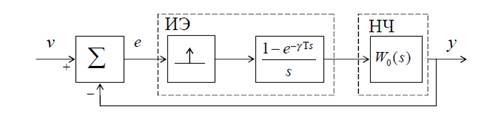
Рис 2.1 Структурная схема линейной импульсной системы
1. Для нахождения передаточной функции разомкнутой импульсной САУ W * ( z ) находим передаточную функцию приведенной непрерывной части:
![]()
К W ( s ) применяется Z-преобразование и получается передаточная функция импульсной системы W * ( z ) = Z { W ( s )} . Преобразуем W 0 ( s ) к виду:
![]()
Представим W 0 ( s ) в виде суммы двух слагаемых ![]()
Применим к W 0 ( s ) Z-преобразование
![]()
Полученную передаточную функцию в конечном виде можно представить следующим образом:
![]()
где обозначено
![]()
![]()
Передаточные функции замкнутой системы находятся по выражениям:
![]()
![]()