Контрольная работа: Анализ систем автоматического управления

Получаем выражение:

где параметры gи fвидны из вышеприведенного выражения.

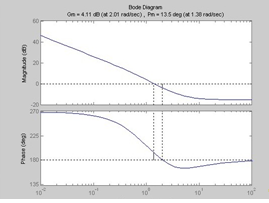
Рис 2.2

4. Рассматриваемая система для всех вариантов является астатической с астатизмом первого порядка и имеет следующую передаточную функцию:

В силу астатизма первого порядка в такой системе статическая ошибка всегда равна нулю, а скоростная е_ск вычисляется по формуле:

и следовательно, е_ск =1,999.

Вычислим коэффициенты ошибок. Величина С₀ =0, а коэффициент ошибки

Где передаточная функция системы по ошибке.

Тогда получим производную:

Подставив в последнее выражение найденные ранее значения и z=1, окончательно получим С₁ =1,999.

5. При входном воздействии вида v ( k ) = l[k] переходный процесс взамкнутой системе можно вычислить с помощью моделирования импульсной системы в Matlab. Для этого необходимо задать передаточную функцию непрерывной части системы в tf - или zpk -форме, преобразовать ее в дискретную с помощью оператора c 2 d при заданном времени дискретизации T , а затем построить переходной процесс системы оператором step . Так же можно построить и логарифмические частотные характеристики импульсной системы -bode . Если задана передаточная функция замкнутой системы в виде:

и периодом дискретизации γ T , то получим

>> w0=tf([0.3 1 0],[0.3 1 1.411]) Transfer function:

0.1 s^2 + s

-------------------

0.1 s^2 + s + 3.738

0.2

>> w1=c2d(w0,0.24)

Transfer function:

z^2 - 0.8801 z - 0.1199

------------------------