Контрольная работа: Анализ систем автоматического управления

2. Устойчивость системы определяется корнями характеристического уравнения замкнутой системы D^* (z) = l+ W^* (z) = 0, которое для нашего случая будет иметь вид:

В соответствии салгебраическим критерием замкнутая система будет устойчива при выполнении неравенств

В неравенстве при известных значениях γ, Т , τ₁ , Т₁ входит величина К₀ . Таким образом, можно выделить отрезок значений К₀ "<К₀ <К₀ , при которых система будет устойчива и далее принять К₀ = 0.5К'₀ . Условия устойчивости будут:

После преобразований и возврата к старым переменным получим:

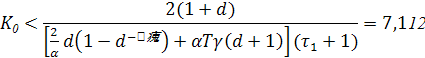
Получим 0<К₀ < 7,112. Таким образом, принимаем К₀ =0.5 К₀ ^’ =3,56.

1. Для построения частотных и логарифмических частотных характеристик в выражении W ^* (z) делаем замену переменной

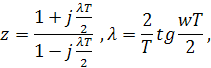
В результате этого получим частотную характеристику W ^* ( jλ ) и далее логарифмическую амплитудно-частотную характеристику L ^* ( λ ) = 20 Lg | W ^* ( jλ )| и фазочастотную характеристику φ^* (λ)= argW ^* ( jλ ), графики которых строятся в логарифмическом масштабе.

Передаточная функция разомкнутой системы имеет вид

Тогда можно воспользоваться следующей последовательностью команд в MATLAB:

>> sys=tf([0.231 0.085],[1 -(1/2.71+1) 1/2.71],1)

Transfer function:

0.231 z + 0.085

---------------------

z^2 - 1.369 z + 0.369

>> sys_tr=d2c(sys,'tustin')

Transfer function:

-0.05332 s^2 - 0.1242 s + 0.4616

--------------------------------

s^2 + 0.9218 s + 2.047e-016