Контрольная работа: Математические модели задач и их решение на ЭВМ

Нижняя цена игры вычисляется α = max_i min_j h_ij = max_i β_j , где α_i - наименьшее значение в i-той строке.

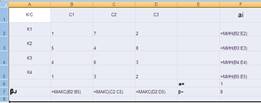
Верхняя цена игры вычисляется β = min_j max_i h_ij = min_j β_j , где β_j = =max_i h_ij - наибольшее значение в j-том столбце.

К\С	С 1	С 2	С 3	αi
К 1	3	7	3	3
К 2	8	1	5	1
К 3	2	6	4	2
α=	1
βj	8	7	5	β=	8

Седловая точка отсутствует, значит нужно составить двойственную задачу.

ЗАДАНИЕ №5

Имеются данные эффективности выпуска новой продукции при различных вариантах решений (стратегий) и различных состояниях среды (природы), таблица 1. Выбрать наилучшее решение, стратегию используя критерии:

1. Максимакса

2. Вальда

3. Сэвиджа

4. Гурвица (коэффициент пессимизма р=0,3)

5. Байеса (вероятности для каждого состояния среды р₁ =0,2, р₂ =0,3, р₃ =0,3, р₄ =0,2)

6. Лапласа

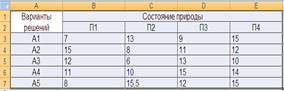
ТАБЛИЦА 1.

ВАРИАНТЫ РЕШЕНИЙ	СОСТОЯНИЕ ПРИРОДЫ
	П1	П2	П3	П4
А1	7	13	9	15
А2	15	8	11	12
А3	12	6	13	10
А4	11	10	15	14
А5	8	15,5	12	15

РЕШЕНИЕ

1. По критерию максимакса наилучшим признается решение, при котором достигается максимальный выигрыш равный

М = max_i max_j h_ij = max_i M_i

Находим М=max_i h_ij , табл.2, т.е.максимальное значение в i-той строке.

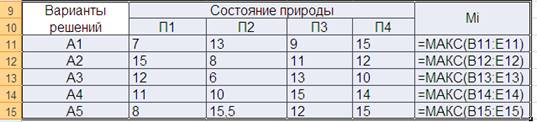
ТАБЛИЦА 2.

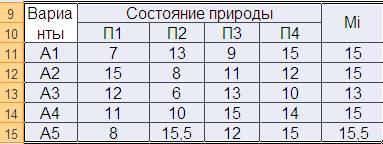
М₁ = 15, М₂ = 15, М₃ =13, М₄ = 15, М₅ = 15,5.

Максимальное значение М = max_i M_i = 15,5, значит решение А5оптимально.

2. Согласно критерию Вальда наиболее предпочтительным является решение, при котором W = max_i min_j h_ij = max_i W_{i .} Находим W_i = min_j h_ij , т.е. минимальное значение W в i-той строке.

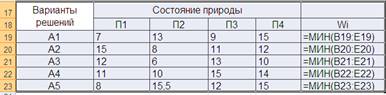
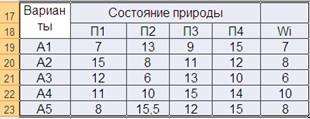
Максимальное значение W=10, следовательно решение А4 является наилучшим.

3. В соответствии с критерием Сэвиджа предпочтение отдается решению, для которого максимальные потери при различных вариантах обстановки окажутся минимальными, т.е. достигается значение:

S = min_i max_j r_ij = min_i S_i .