Контрольная работа: Математические модели задач и их решение на ЭВМ
ta 1 = 0,073525 ‹ tтабл = 1,943. Значит, с уверенностью 94% можно утверждать, что оценка А1 = 0,747263097 не является статистически значимой.
Аналогично проверим для другого параметра. ta 0 = 1,743736 ‹ tтабл = 1,943, значит оценка А0 = 0,123251901 также не является статистически значимой.
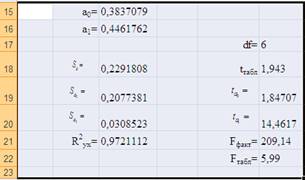

2. Значимость уравнения регрессии в целом и коэффициента тесноты связи R2 определяется с помощью критерия Фишера. Значение оценки R2 получено в предыдущей задаче, R2 = 0,968583448. Фактическое значение Fфакт определяем по формуле: Fфакт = 184,9821.
Табличное значение Fтабл определяем по таблице: F табл = 5,99.
Поскольку Fфакт = 184,9821› Fтабл = 5,99, то с уверенностью 94% делается заключение о том, что уравнение регрессии в целом статистически значимо и статистически значим показатель степени связи R2 , т.е. отвергается нулевая гипотеза о том, что R2 = 0.
ЗАДАНИЕ №8.
Имеются следующие исходные данные:
| Годы | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
| Объем реализации | 10,84 | 11,12 | 10,6 | 11,31 | 11,62 | 12,0 | 12,73 | 11,12 |
Коэффициент достоверности аппроксимации для каждого типа линии тренда
1) Линейная у= 0,1795х – 347,71 R^2=0.4163
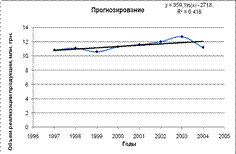
2) Логорифмическая у=359,19 Ln(x)-2718,8 R^2=0.1464
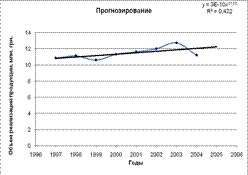
3) Степенная y=3E-102x^31.059 R^2=0.422
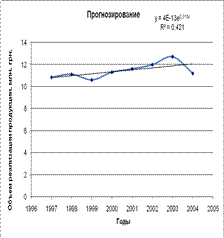
4) Экспонтенциальная у=4Е-13е^0.01558xR^2=0.4218
Как видно из рисунка в 2005г в сравнении с 2004г в среднем реализация продукции увеличилась на 0,42 млн. грн.
ЗАДАНИЕ №9.
Имеются данные испытаний нескольких величин по результатам обследования десяти статистически однородных филиалов фирмы, приведенные в таблице. х1 - фондовооруженность, х2 – энерговооруженность, у – производительность труда.
Выполнить следующее:
1. Построить линейную регрессионную модель при помощи ПЭВМ.
2. Выполнить команду «Регрессия».
3. Определить по результатам команды «Регрессия» значение коэффициента множественной корреляции и детерминации.
4. Проверить статистическую значимость оценок параметров модели.
5. Проверить статистическую значимость оценки степени достоверности взаимосвязи R2 и всей модели в целом.
РЕШЕНИЕ.
1. построить регрессионную модель.
2. выполнить команду «Регрессия», результаты которой показаны ниже.