Контрольная работа: Математические модели задач и их решение на ЭВМ
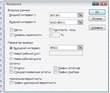

Рис. Результаты команда «Регрессия»
Регрессионная модель принимает вид:
у^ = 0929087*2,9+ - 0,4502*4,5-3,246374
3. Согласно Рис коэффициенты множественной корреляции и детерминации,в данном случае R = 0,993689; R2 = 0,98742.
4. Статистическую значимость оценок параметров модели b,a1 ,а2 осуществим с помощью t-критерия. Для этого определим его табличное значение и его фактические значения для каждого из оцениваемых параметров. По таблице 1 приложения А при уровне значимости 1% найдем табличное значение t-критерия для степеней свободы df= 10-2-1 = 7 и уровня зависимости 7%,т.е. tтабл = 3,143.
Фактическое значение t-критерия для каждого из оцениваемых параметров смотрим на рисунке в столбце t-статистика в нашем случае:
t-a1= 15,73834 ta2= - 0,855361 tb=15,97697
При уровне значимости 7%t-a1= 15,73834> tтабл имеет место равенство: Значит, с уверенностью 99% можно утверждать, что оценка А1 параметра модели является статистически значимой.
Условие ta 2 = -0,855361< tтабл = 3,143 не выполняется, значит утверждаем, что этот критерий статистически не важен.
Условие tв = 15.97697> tтабл = 3,143 выполняется, значит и эта оценка статистически значима в модели.
5. Значимость уравнения регрессии в целом и коэффициента тесноты связи R2 определяем с помощью критерия Фишера. Фактическое Fфакт =274,684752
Табличное значение Fтабл определяем по таблице: Fтабл = 9,55. Условие Fфакт =274684752> Fтабл = 9.55 выполняется, поэтому с вероятностью 99% делается заключение о том, что R2 статистически значим, и уравнение регрессии в целом значимо, т.е. отвергается нулевая гипотеза R2 = 0.