Контрольная работа: Математические модели задач и их решение на ЭВМ

ТАБЛИЦА 4. ВЫИГРЫШИ

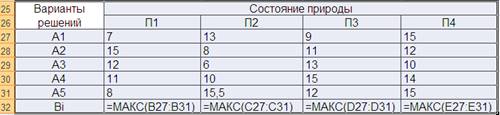
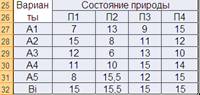
ТАБЛИЦА 5. ПОТЕРИ.

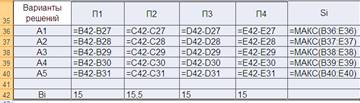
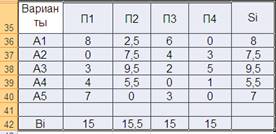
Минимальное значение S = 7. Следовательно оптимальным решением является решение А5.

3. По критерию Гурвица предпочитается то решение, при котором G = max_i { min_i h_ij + (1- p) max_j h_ij } = max_i G_i .

Находим G_i = pW_i + (1-p)M_i , р=0,3 по условию задачи.

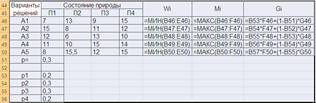
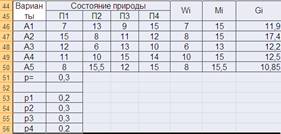
Находим Gmax = 17,4 значит решение А2 является оптимальным.

4. Согласно критерию Байеса наилучшим является решение, при котором достигается максимум математического ожидаемого выигрыша (или минимум среднеожидаемого риска).

Вероятности для каждого состояния среды по условию задачи таковы:

р₁ =0,2, р₂ =0,3, р₃ =0,3, р₄ =0,2. Определяем математическое ожидание выигрышей по каждому решению: МВ1 = ∑р_i h_ij .

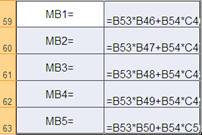
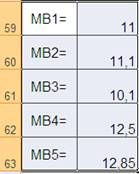
Определяем максимум ожидаемого математического выигрыша. Он равен 12,85, что соответствует четвертому решению, которое, следовательно, и является оптимальным.

Определяем среднеожидаемый риск по каждому решению.

МР_i = ∑p_j r_ij

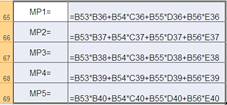
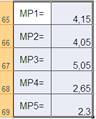
Определяем минимум среднеожидаемого риска. Он равен 2,3, что соответствует пятому решению, которое, следовательно, является оптимальным по данному критерию.

5. Определяем значения для каждого решения по критерию Лапласа.

ВЫИГРЫШИ:

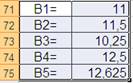
Максимальный выигрыш составит 12,625 что соответствует 2-ому оптимальному решению.

ПРОИГРЫШИ: