Контрольная работа: Математические модели задач и их решение на ЭВМ

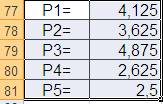
Минимальный проигрыш составит 2,5, что соответствует 5-ому оптимальному решению.

ЗАДАНИЕ №6.

По экспериментальным данным опроса восьми групп семей о расходах на продукты питания, в зависимости от уровня дохода семьи, приведенным в таблице, требуется:

1. Построить линейную однофакторную модель зависимости расходов на питание от дохода семьи.

2. Определить коэффициент корреляции и оценить тесноту связи между доходами семьи и расходами на питание.

3. Определить коэффициент детерминации и коэффициент эластичности, объяснить их смысл.

4. Определить среднюю по модулю относительную ошибку аппроксимации и оценить точность построенной модели.

Доходы семьи (х), тыс.грн.	2.2	3,6	4,2	5,8	6,7	7,9	8,6	10,6
Расходы на продукты (у)	1,2	2,0	2,6	2,9	3,1	3,9	4,5	5

РЕШЕНИЕ. Подготовим вспомогательную таблицу:

Табл 1

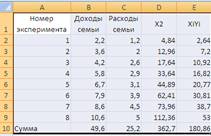
Табл 2

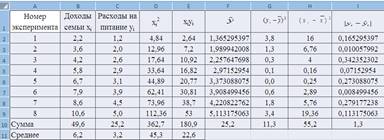
1. По формуле определим коэффициенты а₀ , и а₁ .

А₀ = ∑уi*∑xi^2-∑xiyi*∑xi / n*∑x^2-∑xi*∑xi

Ai=n*∑xiyi-∑xi*∑yi /n*∑x^2-∑xi*∑xi.

Тогда регрессионная модель, согласно формуле, запишется:

Y^=А0+Аi*x

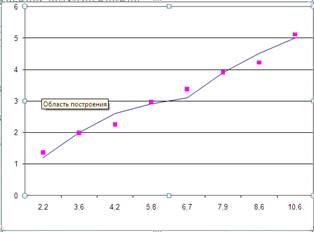
Построим график зависимости и отметим экспериментальные точки.

2. Для полученной модели определим:

А) коэффициент корреляции по формуле и оценим тесноту связи между доходами семьи и расходами на питание.

Xcp=∑xi/nYcp=∑yi/nXYcp=∑xiyi/n

Для этого вычислим средние значения доходов и расходов при помощи EXCEL. Расчеты приведены в табл 2

3. Хср= 49.6/8 = 6.2; Уср= 25.2/8 = 3.2 XcpУср=180,9/8 = 22,6.

Для вычисления среднеквадратических ошибок Sy, Sx имеем формулу: