Контрольная работа: Решение задач по высшей математике

Их ранги равны . Система совместна. Выделим следующую подсистему

Считая и известными, решение подсистемы находим по формулам Крамера . Оно имеет вид

; ,

где , - могут принимать произвольные значения. Пусть , где Тогда ответом будет служить множество

Задача 7

Даны начало и конец вектора . Найти вектор и его длину.

Решение

Имеем , откуда или .

Далее , т.е. .

Задача 8

Даны вершины треугольника , и . Найти с точность до угол при вершине .

Решение

Задача сводится к нахождению угла между векторами и :

, ; . Тогда , .

Задача 9

Даны вершины треугольника , и . Вычислить площадь этого треугольника.

Решение

Так как площадь треугольника равна половине площади параллелограмма, построенного на векторах и как на сторонах, т.е. , то . Найдем векторы и :

; ; .

Вычислим их векторное произведение:

,

,

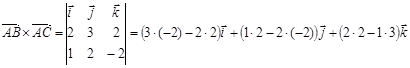Откуда

. Следовательно, (кв. ед.).

Задача 10

Даны вершины треугольной пирамиды , , и . Найти ее объем.