Контрольная работа: Решение задач по высшей математике

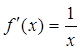Пусть . Тогда . Обозначим: ; . Отсюда . Находим и .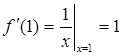

.

Итак, .

Задача 23

Найти .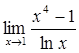

Решение

Подстановка в заданную функцию значения приводит к неопределенности вида . Применив правило Лопиталя, получим:

.

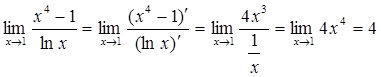Задача 24

Исследовать на экстремум функцию

.

Решение

1. Находим область определения функции:.

2. Находим производную функции: .

3. Находим критические точки, решая уравнение или . Критические точки , .

4. Область определения функции разбиваем критическими точками и на интервалы, в каждом из которых определяем знак , делаем вывод о характере монотонности функции на каждом из интервалов и отмечаем наличие экстремумов.

	+	0	—	0	+
	Возрастает	Max	убывает	Min	Возрастает

При переходе через критическую точку производная меняет знак с “+” на “-”. Значит, в этой точке функция имеет максимум:

.

Аналогично устанавливаем, что

.

Задача 25

Найти наибольшее и наименьшее значения функции

на отрезке .

Решение

1. Находим критические точки заданной функции:

; ; .

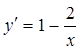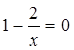2. Убеждаемся в том, что точка принадлежит отрезку.

3. Вычисляем: ; ;.

4. Сравниваем числа ; ; и находим: