Контрольная работа: Решение задач по высшей математике

; ; ; ; ; ; .

Задача 30

Даны функция и точки и . Вычислить:

1) точное значение функции в точке ;

2) приближенное значение функции в точке, исходя из её значения в точке , заменив приращение при переходе от точки к точке дифференциалом ;

3) относительную погрешность, возникающую при замене на .

Решение

По условию , , , . Поэтому , . Находим точное значение функции в точке :

.

Находим приближенное значение :

;

; .

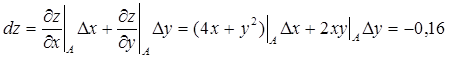Вычисляем относительную погрешность:

.

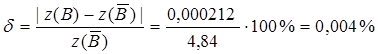Задача 31

Найти экстремумы функции

.

Решение

Находим критические точки:

; ;

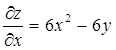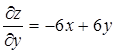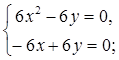
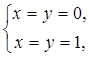
откуда и - точки, где частные производные равны нулю. Исследуем эти точки с помощью достаточных условий

;

;

;

;

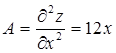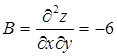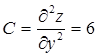. Поэтому экстремума в точке функция не имеет.

, . Поэтому функция в точке имеет минимум: .

Задача 32