Контрольная работа: Решение задач по высшей математике

Подберем коэффициенты и так, чтобы решение удовлетворяло данному уравнению

,

,

.

Приравняв коэффициенты при одинаковых степенях левой и правой частей тождества, получим

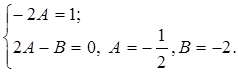
Следовательно, 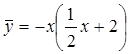, а 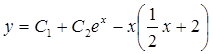- искомое общее решение.

2. Пусть . Тогда частное решение неоднородного уравнения , где - число корней характеристического уравнения, равных .

Задача 44

Найти общее решение уравнения .

Решение

Ищем решение в виде . Решим однородное уравнение . Корни характеристического уравнения равны и . Следовательно, . Частное решение ищем в виде (так как , ). Найдем , а . Подставляя , и в исходное уравнение, получим

,

, , .

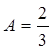Значит, 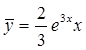- частное решение, а 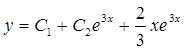- общее решение.

3. Правая часть , где , , - заданные действительные числа. В этом случае частное решение ищется в виде

,

где: и - неизвестные коэффициенты;

- число корней характеристического уравнения, равных .

Задача 45

Найти общее решение уравнения .

Решение

Ищем общее решение в виде . Имеем:

, , , ,

значит, . Функция , поэтому не совпадает с корнями характеристического уравнения . Следовательно,

,

.

Подставив , и в данное уравнение, получим