Имеем , и . Найдем векторное произведение

,

.

Этот вектор скалярно умножим на вектор :

.

Это смешанное произведение можно найти непосредственно по приведенной формуле:

.

Следовательно, объем:

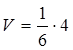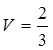, (куб. ед.).

Задача 11

Составить уравнение прямой, проходящей через точки и .

Решение

За первую вершину примем (на результат это не влияет); следовательно,

,

,

,

.

Имеем

, , ,

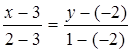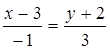Ответ: - общее уравнение искомой прямой.

Задача 12

Составить уравнение прямой, проходящей через точку , параллельно и перпендикулярно прямой .

Решение

Найдем угловой коэффициент данной прямой: . Согласно условиям параллельности и перпендикулярности двух прямых, угловой коэффициент параллельной прямой будет равен , а перпендикулярной прямой будет равен –4 /3. Составляем уравнения искомых прямых:

1) параллельной: , - общее уравнение прямой, параллельной данной;

2) перпендикулярной: , - общее уравнение прямой, перпендикулярной к данной.

Задача 13

Найти расстояние между двумя параллельными прямыми и .

Решение