Контрольная работа: Системы линейных и дифференциальных уравнений
- уравнение медианы ВМ: 
Найдём уравнение высоты АH, проведенной к стороне ВС. Уравнение стороны ВС 
с коэффициентом пропорциональности 
. Коэффициент пропорциональности перпендикулярной прямой будет 
и тогда уравнение высоты принимает вид 
, где К – некая константа, значение которой найдем исходя из условия принадлежности точки А(-3; 1) уравнению высоты AH: 
- уравнение высоты АН: 
Будем искать уравнение биссектрисы угла С.
Прямые АС: 
и ВС: наклонены под острым углом к оси абсцисс (коэффициенты пропорциональности положительны), тогда угол между прямыми АС и ВС будет равен 
, где 
угол между прямыми ВС и АС и осью ОХ соответственно.
По формуле тангенса разности получаем, что
Половина угла С будет 
Тангенс угла наклона биссектрисы к оси ОХ тогда составит:
Уравнение биссектрисы примет вид: 
, где К некая константа, значение которой определим из условия принадлежности точки С(1; 3) биссектрисе, т.е.
Уравнение биссектрисы CL принимает вид 
Для нахождения площади треугольника АВС воспользуемся формулой:
.
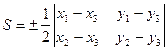Тогда:
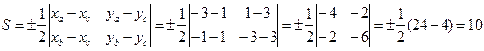кв.ед.
Выполним чертеж:
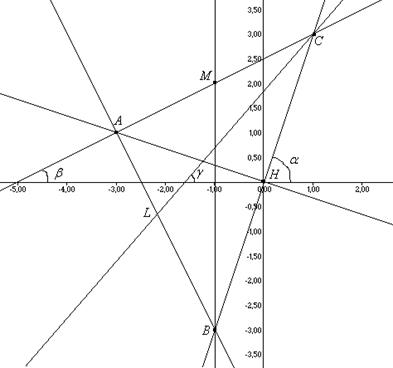
Ответ: АВ: 
АС: ВС: - стороны треугольника
ВМ: 
- медиана треугольника; АН: - высота треугольника;
СL: - биссектриса треугольника; S = 10 кв.ед.
3. Даны координаты точек А1 ,A2 ,А3 ,A4
Найти длину ребра А1 А2. Составить уравнение ребра А1 А4 и грани А1 А2 А3. Составить уравнение высоты опущенной из точки А4 на плоскость А1 А2 А3. Найти площадь треугольника А1 A2 A3 . Найти объем треугольной пирамиды А1 A2 А3 A4
| N | Координаты точек | |||
| Вар | A1 | A2 | A3 | A4 |
| 2.19 | (8;6;4) | (10;5;5) | (5;6;8) | (8;10;7) |
Решение:
Воспользуемся формулой для вычисления расстояние между двумя точками:
Наши точки А1 (8; 6; 4) и A2 (10; 5; 5):
ед.
Длина ребра А1 А2 равна 
ед.
Составим уравнение прямой проходящей через точки А1 (8; 6; 4) и A4 (8; 10; 7).
Для этоговоспользуемся уравнением:
, т.е. А1 А4 : 
.