Контрольная работа: Системы линейных и дифференциальных уравнений

При система принимает вид:

Общее решение этой системы , где любое число.

Пусть, например, , тогда собственный вектор, соответствующий собственному числу , имеет вид: .

Аналогично при получаем систему

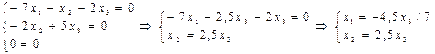
общее решение которой 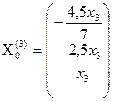, где любое число.

Пусть , тогда собственный вектор, соответствующий собственному числу , имеет вид: .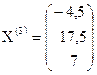

Ответ: , , .

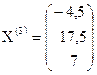5. Решить систему методом Жорданa - Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.

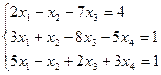
Решение:

Преобразуем расширенную матрицу системы к диагональному виду:

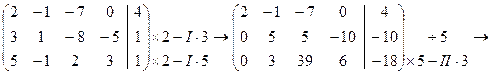
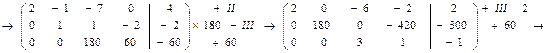
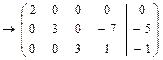
откуда получаем следующую систему

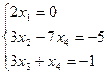и

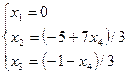- общее решение исходной системы уравнений.

Частные решения получим присвоив конкретные значения переменной х₄ :

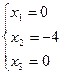тогда: , т.е. решением будет вектор (0; -4; 0; -1)

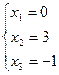тогда: , т.е. решением будет вектор (0; 3; -1; 2).

Выполним проверку общего решения:

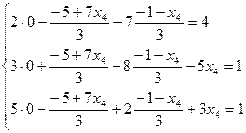
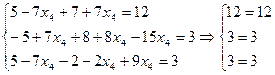- верные равенства.

Ответ: 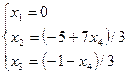; (0; -4; 0; -1); (0; 3; -1; 2).

к/р № 2

1. Найти следующие пределы.

а) б)

Решение:

а) - неопределенность с бесконечностью. Раскроем скобки, приведем подобные и разделим числитель и знаменатель дроби на максимальную степень х. Получим:

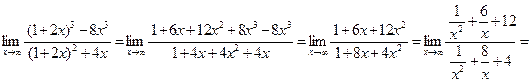
б) - неопределенность . Избавимся от обнуляющего множителя, для этого числитель разложим на множители, а к знаменателю применим эквивалентную бесконечно малую: при . Получим: