Контрольная работа: Системы линейных и дифференциальных уравнений

6) Критические точки:

Найдем производную функции y и решим уравнение yґ = 0.

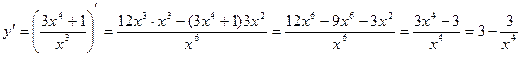
т.е. точка: (-1; -4) – точка максимума и (1; 4) - точка минимума.

7) Точки перегиба:

Найдем вторую производную функции y и решим уравнение yґґ = 0.

, значит - нет решений.

При x > 0 функция выпуклая, при x < 0 вогнутая.

8) Построим график функции:

4. Найти

???????? ??????? Z ? ????? ?.

уравнение матрица функция вектор дифференциальный

Решение:

Градиентом функции z в точке М является вектор grad (z) =

Т.е. grad(z) = .

Ответ: grad (z) = .

5. Вычислить неопределенные интегралы.

а) б) с) .

Решение:

а)

Рассмотрим интеграл :

Тогда