Контрольная работа: Системы линейных и дифференциальных уравнений

б) Определить область сходимости ряда.

а) б) .

Решение:

а) - рассмотрим ряд из абсолютных величин .

Поскольку , то .

Ряд сходится как обобщенный гармонический ряд степени р = 2 >1, следовательно и меньший ряд также сходится.

Исходный ряд сходится абсолютно.

б) Для степенного ряда вида интервалом сходимости будет интервал (x₀ – R; x₀ + R), где 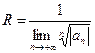- радиус сходимости степенного ряда.

Для нашего ряда получим: x₀ = 2 и общий член .

Тогда: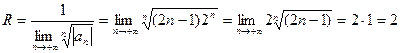

Получили интервал сходимости (2 – 2; 2 + 2) или (0; 4).

Рассмотрим концы интервала.

х = 4: - расходящийся гармонический ряд.

х = 0: - условно сходящийся ряд Лейбница.

Ответ: а) сходится абсолютно; б) [0; 4).