Контрольная работа: Высшая математика 4

ЗАДАЧА 1. Вычислить пределы функций а) —д):

а) 1..

►==.

2. .

►.====0.

3. ..

►.====-∞.

б) .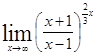

Решение.==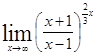

==

===

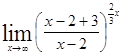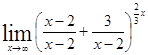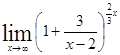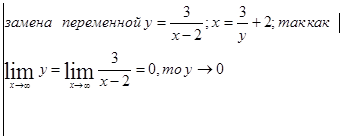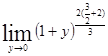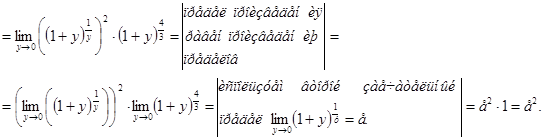
Предел вычислен подстановкой

Предел не может быть вычислен подстановкой , поскольку в результате подстановки получается неопределенность .

в) .

Анализ задачи. Подстановка числа 2 вместо показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность . Для этого можно либо провести тождественные преобразования выражения , либо применить правило Лопиталя.

Решение. Выражение является сопряженным по отношению к выражению , а выражение - по отношению к . Умножая числитель и знаменатель дроби на произведение сопряженных выражений ()·(), и используя формулу разности квадратов , получаем

Другое решение задачи. Воспользуемся правилом Лопиталя

Ответ:

Анализ задачи. В данном случае, непосредственное применение те­оремы о пределе частного невозможного, поскольку, как показывает подстановка числа. -3 вместо x и предел числителя и предел знаме­натели равны пулю.

и

Таким образом, рассматриваемый предел представляет собой неопределённость вида и для решения задачи требуется про­вести тождественные преобразования выражения, находящего­ся под знаком предела.

Решение. Разложим числитель и знаменатель на множители, пользуясь следующей теоремой: если— корни квадратного трехчлена, то,

= Решаем квадратное уравнение, находя его дискриминант D.

Отсюда,

Аналогично,

Поэтому,

Преобразуем выражение находящиеся под знаком предела:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--