Контрольная работа: Высшая математика 4

►

.◄

ЗАДАЧА 3. Исследовать функцию и построить график

Исследовать функцию и построить её график.

►Исследуем данную функцию.

1. Областью определения функции является множество .

2. Ордината точки графика .

3. Точки пересечения графика данной функции с осями координат:

4. Легко находим, что

.

Находим наклонные асимптоты:

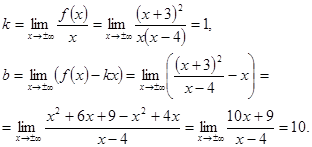
Таким образом, существует единственная наклонная асимптота

5. Исследуем функцию на возрастание, убывание, ло­кальный экстремум:'

y= 2(х + 3)(x-4)-(x + 3)² _ 2x² – 2x - 24 – х² - 6х - 9 =
(х-4)² (x-4)²

=.

Из у' = 0 следует х^г — 8х — 33 = 0, откуда = 11, х₂₌ — 3. В интервале (—∞; — 3) y'> 0, следовательно, функция возрастает в этом интервале; в (—3; 4) y'<0, т. е. функция убывает. Поэтому функция в точке х = —3 имеет локальный максимум: у( —3) = 0. В интервале (4; 11)

у' < 0, следовательно, функция убывает на этом интер­вале; в (11; +∞) у'>0, т. е. функции возрастает. В точке = 11 имеем локальный минимум: y(ll) =28.

6. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем

=

==.

Очевидно, что в интервале (—∞; 4) y"< 0, и в этом интервале кривая выпукла; в (4; +∞)

у" > 0, т. е. в этом интервале кривая вогнута. Так как при х = 4 функция не определена, то точка перегиба отсутствует.

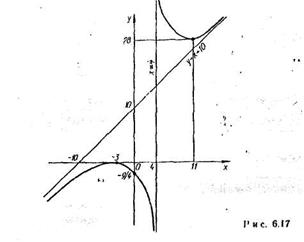
7. График функции изображен на рис. 0.17

ЗАДАЧА 4. Вычислить неопределенные интегралы а) – в)

а)

1.

►◄

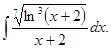
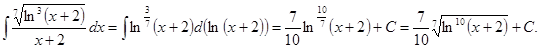2.

►