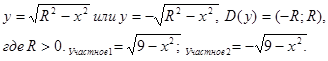Контрольная работа: Высшая математика 4

Описанный метод решения можно схематично представить в виде формулы:

ЗАДАЧА 6. Найти общее решение дифференциального уравнения Построить графики двух частных решений этого уравнения.

Решение. 1). Преобразуем уравнение к виду

Равенство (у² + х² ) = С показывает, что С > 0. Положим С =∙ R² ,где R > 0 — другая произвольная постоянная. Тогда

у² + х² = R² .

3). Разрешим, предыдущее уравнение относительно у и найдём область определения решения:

Рис. к задаче 6.

D(у) =>0. Графики решений — дуги концентрических окружностей произвольного радиуса с центром в на­чале координат (см. рис.).

4). В данном случае, уравнение не имеет решений. Поэтому решений вида

y = а нет.

Ответ:

Линейные дифференциальные уравнение второго порядка с постоянными коэффициентами. Уравнение вида

(7) у" + by' + су=0,

где b и с — некоторые числа, называется линейным однородным диф­ференциальным уравнением второго порядка с постоянными коэффи­циентами. Общее решение этого уравнения в зависимости от знака дискриминанта

характеристического уравнения

. (8) k² + bk + c = 0

имеют следующий вид:

A) если D > 0, где k =α, к=β — два различных действительных корня (α≠β) характеристического уравнения (8);

Б) , если D = О,

где α— единственный корень характеристического уравнения;

B) если D < О,

где

Общее решение линейного неоднородного дифференциаль­ного уравнения второго порядка с постоянными коэффициентами

(9)

является суммой некоторого его частного решения и общего решения

. однородного уравнения (7), т. е.