Контрольная работа: Высшая математика
Рассчитаем оптимальные значения параметров системы.
Найдем оптимальный размер партии:
q =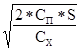 
= 
» 1735 шт.
Найдем число поставок в год:
Nо = S / q = 62000 / 1735 = 35,7 » 36 раз
Найдем период между поставками:
То = 360 / 36 = 10 дней
Найдем издержки пополнения:
ИП о = СП * N = 1650 * 36 = 59400 руб.
Найдем издержки хранения:
ИХ о = CX * 
= 68 * 1735 / 2 = 58990 руб.
Найдем суммарные издержки
Ио = ИП о + ИХ о = 59400 + 58990 = 118390 руб.
Построим график запасов:
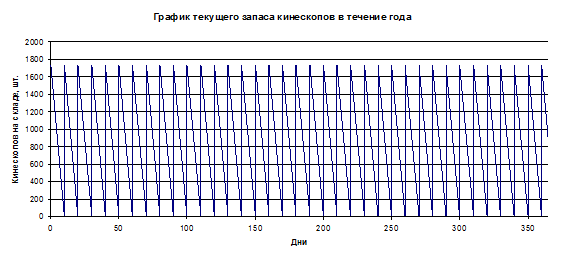
Рис. 1
Рассмотрим функции издержек.
Годовые издержки пополнения запасов ИП (q) = СП * 
являются обратной гиперболической функцией, которая монотонно убывает с увеличением размера партии q. С возрастанием q скорость убывания падает.
Годовые издержки хранения ИХ (q) = CX * являются линейной функцией, которая монотонно возрастает с увеличением размера партии q. Минимальное значение функции нулевое. С возрастанием q скорость увеличения издержек хранения не изменяется.
Суммарные издержки являются суммой двух предыдущих функций. В силу этого, функция сначала убывает – когда издержки пополнения запасов существенно выше издержек хранения, а после выравнивания размеров издержек начинает возрастать – когда издержки хранения превышают размер издержек пополнения. Функция суммарных издержек имеет один минимум в районе примерного равенства входящих в нее функций.
Построим графики изменения трех видов издержек как функций размера партииq:
Рис..2
Задача 3
Фирма собрала сведения об объемах продаж своей продукции (Yi ) за 6 последних месяцев (Xi =1...6) и представила их в виде таблицы. Перед отделом маркетинга поставлена задача аппроксимировать эмпирические данные подходящей функцией, чтобы использовать ее для целей краткосрочного прогнозирования (на один и два месяца вперед, Xj =7, 8).
Таблица 1 - Данные о помесячных объемах продаж фирмы
| № | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 |
| 12 | 14 | 13 | 11 | 14 | 13 | 16 |
Указания к задаче 3:
1) выполните аппроксимацию эмпирических данных линейной функцией у = a0 x + a1 ;
2) выведите нормальные уравнения метода наименьших квадратов для линейной функции;