Контрольная работа: Высшая математика

4) для расчета параметров аппроксимирующей линейной функции составьте таблицу.

Таблица.2 - Параметризация аппроксимирующей линейной функции.

i	Xi	Yi	Xi 2	Xi Yi
1
2
3
4
5
6
Сумма

5) запишите выражение для аппроксимирующей линейной функции и рассчитайте ее значения о точках X_i = 1...8; результаты расчетов оформите в виде таблицы;

6) изобразите на одном рисунке в большом масштабе график аппроксимирующей линейной функции и нанесите эмпирические точки.

Решение:

Аппроксимацию эмпирических данных будем выполнять линейной функцией

у = a₀ x + a₁

Сущность метода наименьших квадратов состоит в подборе таких a₁ и a₀ , чтобы сумма квадратов отклонений была минимальной. Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений будет функцией F этих параметров: F(a₀ , a₁ ) = или F(a₀ , a₁ ) =

Для отыскания минимума приравняем нулю частные производные по каждому параметру:

=

=

Выполнив элементарные преобразования сумм, получим систему из двух линейных уравнений относительно a₁ и a₀ :

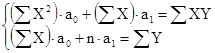
Решим данную систему методом Крамера:

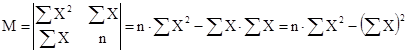
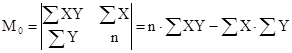
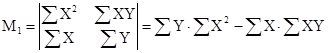
Тогда можно вывести формулы расчета параметров:

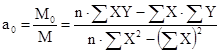
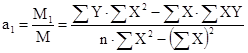
Построим расчетную таблицу

Таблица 3 – Расчетная таблица

i	Xi	Yi	Xi 2	Xi Yi
1	1	14	1	14
2	2	13	4	26
3	3	11	9	33
4	4	14	16	56
5	5	13	25	65
6	6	16	36	96
Сумма	21	81	91	290

Найдем значения параметров:

Тогда формула аппроксимирующей линейной функции будет равна

= 0,3714·X_i + 12,2

Найдем значения аппроксимирующей функции:

Таблица 4 – Расчет значений аппроксимирующей функции

i	Xi
1	1	12,5714
2	2	12,9428
3	3	13,3142
4	4	13,6856
5	5	14,057
6	6	14,4284
7	7	14,7998
8	8	15,1712