Контрольная работа: Высшая математика

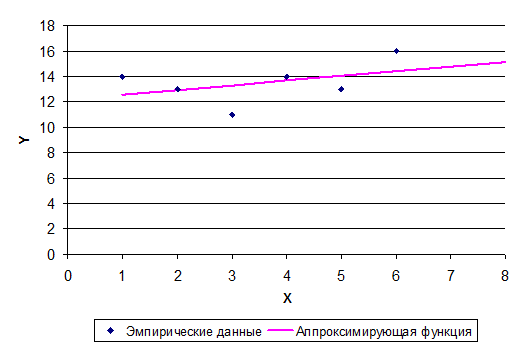
Рис.1

Задача 4

Найти приращение и дифференциал функции y=a₀ x³ +a₁ x² +a₂ x (таблица). Рассчитать абсолютное и относительное отклонения dy от Δy.

Решение:

y=4x³ –2x² –3x

Приращение функции

y(x+Δx)–y(x)= 4(x+Δx)³ –2(x+Δx)² –3(x+Δx) – (4x³ –2x² –3x)=

=4(x³ +3x² Δx + 3xΔx² + Δx³ )–2(x² +2 xΔx +Δx² )–3x–3Δx –4x³ +2x² +3x=

=4x³ +12x² Δx + 12xΔx² + 4Δx³ –2x² –4 xΔx –2Δx² –3Δx –4x³ +2x² =

=12x² Δx + 12xΔx² + 4Δx³ –4 xΔx –2Δx² –3Δx =

=(12x² –4 x–3)Δx+((12x–2)Δx² + 4Δx³ )

Линейная по Δx часть приращения есть дифференциал, то есть

dy=(12x² –4 x–3)Δxили заменяя Δx на dx получим dy=(12x² –4 x–3)dx

Абсолютное отклонение:

Δy– dy = (12x² –4 x–3)Δx+((12x–2)Δx² + 4Δx³ )– (12x² –4 x–3)Δx=(12x–2)Δx² + 4Δx³

Относительное отклонение:

Задача 5

Используя дифференциал, рассчитайте приближенное значение функции , оцените относительную погрешность и вычислите значение с 6 знаками.

n=3, x=63

Решение:

Возьмем

=64

=>

Тогда