Курсовая работа: Асимптотика решений дифференциальных уравнений
Ряд Тейлора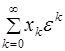 
может расходиться на любом отрезке 
, но он будет асимптотическим рядом для функции 
. Действительно,
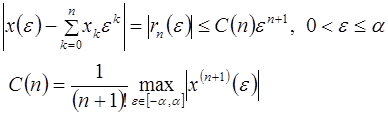(2.3)
Пример 2 . Рассмотрим функцию
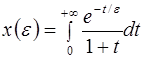
Интегрируя по частям, получаем
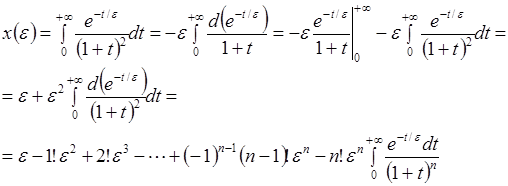
Таким образом,
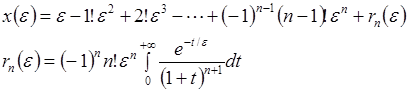
Ряд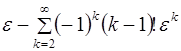 
расходится при любом 
, но является асимптотическим для функции , так как
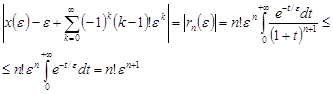
Замечание . Асимптотический ряд может быть полезен при вычислении значений функции при малых или больших значениях параметра .
Рассмотрим функцию примера 2. Вычисляя интеграл численно, получаем при 
Вычисляя частичные суммы асимптотического ряда и оценивая разности 
, получаем первые 20 чисел
0.0015633, -0.0004366, 0.0001633, -0.0000766, 0.0000433, -0.0000287, 0.0000217,
-0.000186, 0.0000177, -0.0000186, 0.00002133, -0.0000266, 0.0000357, -0.0000515,
0.0000793, -0.0001299, 0.0002257, -0.0004145, 0.0008020
Наилучшее приближение дает девятая частичная сумма.
На рис. 1 изображен графически характер приближения частичных сумм к значению. На горизонтали оси откладывается номер 
, по вертикали частичная сумма 
.
рис. 1
Пусть 
банаховы пространства 
и при 
задано семейство операторов 
. Рассмотрим при 
уравнение 
. Допустим, что это уравнение при каждом 
имеет единственное решение
