Курсовая работа: Асимптотика решений дифференциальных уравнений
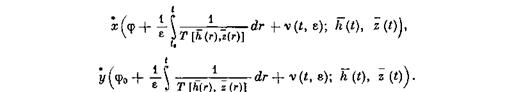
Здесь ф0 определяется из соотношений постоянная величина, v(t, e) — решение уравнения:
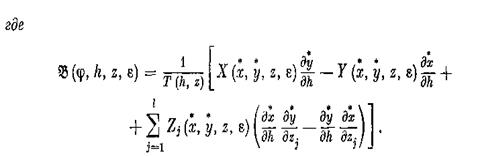
Доказательство. Прежде всего установим ряд свойств решения (2.6) системы (2.2), имеющих место при тех требованиях гладкости, которые указаны в формулировке теоремы 1.
Свойство 1. Периодом решения (2.6) является функция
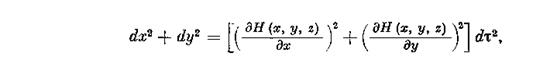следовательно, эта функция непрерывна в Gh вместе со всеми своими частными производными до второго порядка включительно. Действительно, из (2.2) следует соотношение интегрирование которого дает формулу (2.9). Из указанной в условиях теоремы гладкости функций
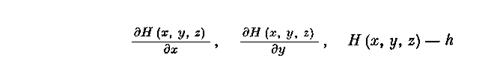
следует соответствующая гладкость функции Т( h , z ) в Gh .
Свойство 2. Функции 
определены и непрерывны в области — 
вместе со всеми своими частными производными до второго порядка включительно.
В самом деле, в силу указанной гладкости правых частей системы (2.2), из (2.5), по теореме о неявных функциях, следует, что функции а (/г, z), Р (/г, z ) непрерывны в Gh вместе со всеми своими частными производными до второго порядка включительно. Далее, из теорем о существовании и единственности, о непрерывности и непрерывной дифференцируемости решений системы обыкновенных дифференциальных уравнений по начальным значениям и по параметрам следует, что функции 
вместе со всеми своими частными производными до второго порядка включительно, непрерывны в области — 
. Следовательно, функции 
обладают свойством 2 как сложные функции.!
Свойство 3. Пусть D — некоторая ограниченная замкнутая об
ласть, содержащаяся в Gh . Тогда на множестве — 
функции 
вместе со всеми своими частными производными до второго порядка включительно ограничены.
Свойство 3 является следствием свойства 2, так как периодичность функций 
позволяет рассматривать их в замкнутой и ограниченной области
Свойство 4.
так как решение (2.6) описывает фазовую траекторию (2.3). Дифференцирование соотношения (2.10) по Zj дает Свойство 5.
(2.10)
где
(2.11)
Свойство 6.
(2.12)
