Курсовая работа: Асимптотика решений дифференциальных уравнений

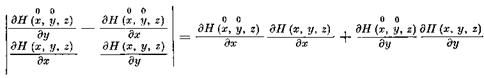
отличен от нуля в точке (х, у, z , /г), так как точка (х, ?/, z ) не является положением равновесия системы (2.2). Поэтому, по теореме о неявных функциях, в некоторой окрестности Г° точки (х, у, z , h ) (Г°С Г) система (2.5) разрешима относительно х и у:

причем

являются однозначными функциями от /г, zi ,. .., z_x , непрерывными по совокупности этих переменных вместе со всеми своими первыми частными производными. Следовательно, целые фазовые траектории системы (2.2), проходящие через точки

составляют искомую окрестность G траектории (2.4). Пусть

— решение системы (2.2) с начальными условиями

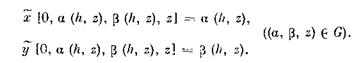
Решение (2.6) системы (2.2) является периодическим, поскольку описывает замкнутую траекторию (2.3). Тогда, полагая получим:

2. Изучение системы (2.1). Исследуем решение

системы (2.1) с начальными условиями

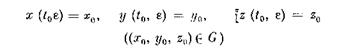на конечном промежутке времени Uo, L]. Имеет место

ТЕОРЕМА 1. Пусть функции 1

определены и непрерывны в вместе со всеми своими частными произвооными до второго'порядка включительно, а функции непрерывны в вместе со всеми своими первыми частными производными. Тогда существует число такое, что при любом на конечном промежутке времени [ to , L ]:

1) решение системы (2.1) остается в G и функции h с точностью до величин порядка О (г) совпадают соответственно с функциями представляющими собой решение следующей автономной системы не зависящих от е обыкновенных дифференциальных уравнений, правые части которых выражаются через правые части системы (2.1):

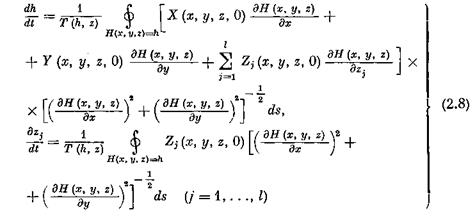
циал дуги фазовой траектории (2.3), интегрирование ведется при произвольно фиксированной паре

Предполагаем, что решениесистемы

(2.8)

имеет начальныезначения