Курсовая работа: Асимптотика решений дифференциальных уравнений
Функция О2 (х, у, е), в силу указанной в условиях теоремы гладкости правых частей системы (2.1), является однородной квадратичной относительно х, у, е с ограниченными в Gooкоэффициентами, и поэтому
![]()
![]()
постоянная величина).
С другой стороны, по формуле Тейлора, в силу (2.54) имеем в G00
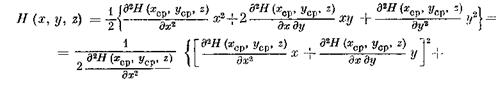
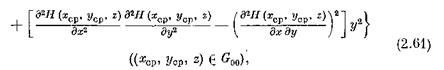
и так как при (х, у, z )
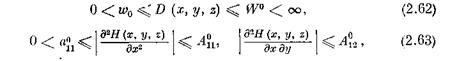
то соотношение (2.61), в силу (2.57), дает на [£0 , t (е) ]:
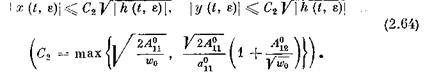 |
Но, по (2.56) - (2.58) и (2.63),

![]()
Соотношения
дают:
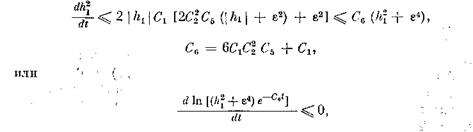
![]()
откуда следует, что на отрезке
Но так как, в силу
![]()
![]()
т. е. окончательно, по (2.64), (2.67),
![]()
2. Регулярные возмущения.
2.1 Асимптотические методы
Пусть задано банахово пространство ![]() и отображение
и отображение ![]() .
.
Определение . Будем ряд 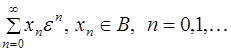 называть асимптотическим рядом для функции
называть асимптотическим рядом для функции ![]() , если для любого
, если для любого ![]() найдутся числа
найдутся числа ![]() и
и ![]() такие, что
такие, что
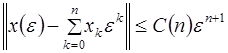 при
при ![]() (2.1)
(2.1)
Пример 1 . Если функция ![]() имеет производные всех порядков в точке
имеет производные всех порядков в точке ![]() , то справедливо формула Тейлора
, то справедливо формула Тейлора