Курсовая работа: Асимптотика решений дифференциальных уравнений

и так как точка { h (£, е), z ( t , е)} остается в G_hp CZG_h , то на отрезке [ t_Q , L ] при любом 8 g (0, е₀ ] решение {х ( t , е),?/ (£, е), z (£, г)} системы (2.1) остается в G, причем, по свойству 3,

В силу же (2.13),

и потому соотношения (2.39), (2.40) доказывают первую часть теоремы 1. Докажем вторую часть теоремы 1. По формуле конечных приращений, из (2.41) получаем:

Возникает вопрос, как ведут себя решения системы (2.1) во всей указанной окрестности Go (включая и положения равновесия {/ (z), g (z), z} системы (2.3)). На этот вопрос отвечают теорема 1 и нижеследующие теоремы 2 и 3.

ТЕОРЕМА 2. Пусть в окрестности Go выполнены условия теоремы 1, касающиеся гладкости правых частей системы (2.1). Тогда найдется число 8° у> О, такое, что при любом г £ (0, е°] (е° <^ а) на конечном промежутке времени [ to , L ] решение {х ( t , е), у ( t , е), z ( t , г)} системы (2.1) с начальными условиями вырожденной системы

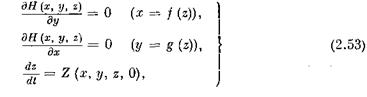
остается в Go и с точностью до величин порядка О (г) совпадает с решением

проходящим при t — to через то же положение равновесия

(предполагается, что решение {х ( t ) , у ( t ) , z ( t )} остается в G на [ t ₀ , L]). Доказательство. Не нарушая общности рассуждений, будем считать, что в Go

1 1 так как замена переменных х, у, z_x ,..., z_t на х, у, z_1? .... z> и Н

на Я¹ , где

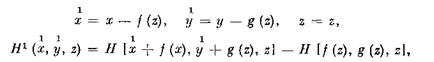
сохраняет вид системы (2.1), но дает условия (2.54). Следовательно, в силу.

Это решение на конечном промежутке времени [ t ₀ , L ] составляет некоторое замкнутое ограниченное множество F_Q CZG ₀ и поэтому найдется ро > 0 такое, что G₀₀ С G ₀ ( G_{Q 0} — р₀ -окрестность F ₀ ).

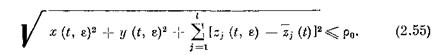
Положим

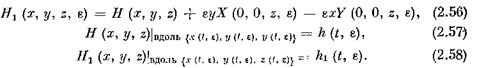
В силу (2.56) и (2.1), вдоль решения {х (£, е), у ( t , е), z ( t , &)} имеем:

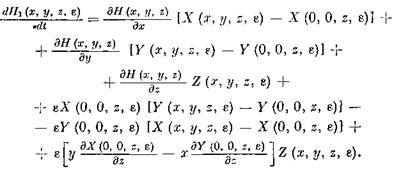
Следовательно, по формуле Тейлора, примененной к функциям

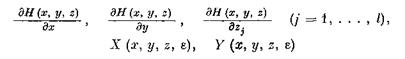
относительно х, у в G₀₀ , в силу (2.54), (2.58), получим на [ t ₀ , t ^ (г)]: