Курсовая работа: Беселеві функції

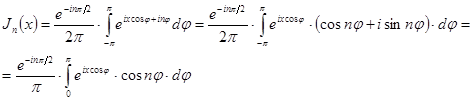
(з огляду на, що є парна функція від , а є непарна функція від ). Підстановка дає:

,

де є, мабуть, поліном n-й ступеня (поліном Чебишева), тому що з формули Муавра видно, що є поліном n-й ступеня відносно . Але

і, заміняючи в першому із цих інтегралів на , одержимо:

Тому що й на мають похідні всіх порядків, то до двох останніх інтегралів застосовні формули (29) і (29`), і ми одержуємо:

;

але ; , отже,

.

Отже, маємо шукане асимптотичне подання беселевої функції першого роду із цілим індексом для більших значень аргументу:

при . (30)

Ця формула показує, що з точністю складається до порядку, що, є загасаючою гармонікою із хвилею постійної довжини й амплітудою, що убуває обернено пропорційно квадратному кореню з абсциси.

Зокрема,

при ; (30`)

при . (30'')

Графіки цих функцій зображені ні малюнках 1 і 2.

Розглянемо кілька прикладів рішення рівняння Беселя.

1. Знайти рішення рівняння Беселя при

,

задовольняючим початковим умовам при , і .

Рішення.

На підставі формули (5') знаходимо одне приватне рішення:

.

2. Знайти одне з рішень рівняння:

, .

Рішення.

Зробимо заміну