Курсовая работа: Беселеві функції

. (17)

Виробляюча функція системи Беселевих функцій із цілими індексами

Покажемо, що для системи Беселевих функцій першого роду із цілими індексами (…) виробляюча функція є:

.

Маємо:

, ,

звідки після по членного перемножування цих рівностей знайдемо:

(тому що в передостанній внутрішній сумі й були зв'язані залежністю , то ми могли покласти , одержавши підсумовування по одному індексі ). В останній внутрішній сумі підсумовування виробляється по всіх цілих , для яких , отже, при це буде ; при це буде . Таким чином, у всіх випадках внутрішня сума є в силу формул (5`) і (5```). Отже,

, (18)

але це й доводить, що є виробляюча функція для системи .

Виведемо деякі наслідки з формули (18). Думаючи в ній , одержимо:

,

звідки після поділу дійсної й мнимої частини (з огляду на, що )

(18`)

(18``)

Заміняючи в (18`) і (18``) на , знайдемо:

, (18```)

. (18````)

Інтегральне подання Jn(x)

Тому що, по доведеному, при маємо , те по формулі (17) одержуємо (використовуючи в перетвореннях формули Ейлера):

де прийнято в увагу, що є парна функція від є непарна функція від . Отже, доведено, що для будь-якого цілого числа

. (19)

Формула (19) дає подання Беселевих функцій із цілим індексом у вигляді певного інтеграла, що залежить від параметра . Ця формула називається інтегральним поданням Беселя для , права частина формули називається інтегралом Беселя. Зокрема, при знайдемо:

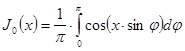. (19`)

5. Ряди Фур'є-Беселя

Розглянемо на якому-небудь інтервалі (кінцевому або нескінченному) два диференціальних рівняння

, , (20)